题目内容
12.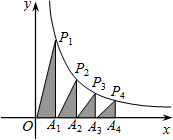 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3…=A2014A2015=1,过点A1、A2、A3、…、A2015分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、…P2015,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、…A2014P2015A2015,并设其面积分别为S1、S2、S3、…S2015,则S2015的值为$\frac{1}{2015}$.
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3…=A2014A2015=1,过点A1、A2、A3、…、A2015分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、…P2015,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、…A2014P2015A2015,并设其面积分别为S1、S2、S3、…S2015,则S2015的值为$\frac{1}{2015}$.
分析 根据反比例函数y=$\frac{k}{x}$中k的几何意义再结合图象即可解答.
解答 解:因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,S=$\frac{1}{2}$|k|=1.
又因为OA1=A1A2=A2A3=A3A4=A4A5
所以S1=1,
S2=$\frac{1}{2}$S1=$\frac{1}{2}$,
S3=$\frac{1}{3}$S1=$\frac{1}{6}$,
S4=$\frac{1}{4}$S1=$\frac{1}{8}$,
S5=$\frac{1}{5}$S1=$\frac{1}{10}$.
…
依此类推:Sn的值为$\frac{1}{n}$.
当n=2015时,S2015=$\frac{1}{2015}$.
故答案是:$\frac{1}{2015}$.
点评 本题主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|.

练习册系列答案
相关题目
20.在实数:-0.3,$\sqrt{1}$,2.010010001…(0的个数依次递增),4.$\stackrel{••}{21}$,2π,$\frac{22}{7}$中,无理数有( )
| A. | 1 | B. | 2个 | C. | 3个 | D. | 4个 |
17.把分式$\frac{2a}{a+b}$中的a、b都扩大4倍,则分式的值( )
| A. | 扩大8倍 | B. | 不变 | C. | 缩小4倍 | D. | 扩大4倍 |
4.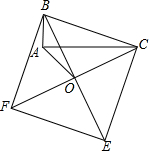 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,对角线交于点O,连结AO,如果AB=4,AO=4$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,对角线交于点O,连结AO,如果AB=4,AO=4$\sqrt{2}$,那么AC的长等于( )
 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,对角线交于点O,连结AO,如果AB=4,AO=4$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,对角线交于点O,连结AO,如果AB=4,AO=4$\sqrt{2}$,那么AC的长等于( )| A. | 12 | B. | 16 | C. | 4$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
 如图,点O为直线AB上一点,∠AOC=50°,OD平分∠AOC.
如图,点O为直线AB上一点,∠AOC=50°,OD平分∠AOC. 如图,将Rt△ABC绕点A逆时针旋转34°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠BB′C′的度数为17°.
如图,将Rt△ABC绕点A逆时针旋转34°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠BB′C′的度数为17°.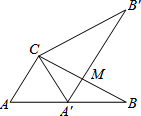 如图,△ABC中,∠ACB=90°,∠B=30°,BC=6,三角板绕C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则BM的长为3.
如图,△ABC中,∠ACB=90°,∠B=30°,BC=6,三角板绕C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则BM的长为3. 设E、F分别在正方形ABCD的边BC,CD上滑动保持且∠EAF=45°.若AB=5,求△ECF的周长.
设E、F分别在正方形ABCD的边BC,CD上滑动保持且∠EAF=45°.若AB=5,求△ECF的周长.