题目内容
1. 设E、F分别在正方形ABCD的边BC,CD上滑动保持且∠EAF=45°.若AB=5,求△ECF的周长.
设E、F分别在正方形ABCD的边BC,CD上滑动保持且∠EAF=45°.若AB=5,求△ECF的周长.
分析 将△ABE绕点A逆时针旋转90°至△ADG.首先证明△AFE≌△AFG,进而得到EF=BE+FD,从而将三角形的周长转化为BC+CD的长.
解答 解:如图所示,将△ABE绕点A逆时针旋转90°至△ADG.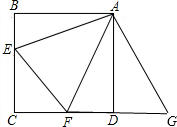
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中,
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠FAG}\\{AF=AF}\end{array}\right.$,
∴△AFE≌△AFG(SAS),
∴EF=FG,即:EF=BE+DF.
∴△EFC的周长=EC+CF+EF=EC+CF+BE+FD=BC+CD=5×2=10.
点评 考查正方形的性质、全等三角形的判定及其性质为核心构造而成;解题的关键是作辅助线,构造全等三角形,将三角形的周长转为BC+CD的长.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
9.ax2+bx+c=0是关于x的一元二次方程的条件是( )
| A. | a,b,c为任意实数 | B. | a,b不同时为0 | C. | a不为0 | D. | b,c不同时为0 |
13.下列各组线段,能组成三角形的是( )
| A. | 3,3,3 | B. | 3,2,5 | C. | 3,3,6 | D. | 3,2,6 |
10.直线y=kx+b与直线y=2x+2014平行,且与y轴交于点M(0,4),则其函数关系式是( )
| A. | y=-2x-4 | B. | y=2x+4 | C. | y=-2x+4 | D. | y=2x-4 |
11.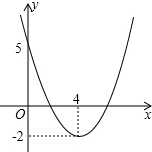 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
 二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )
二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是( )| A. | m≥-2 | B. | m≥5 | C. | m≥0 | D. | m>4 |
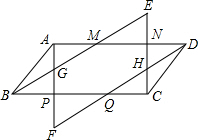 如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF分别交BE、BC、DF于G、P、F点;CE分别交DF、AD、BE于H、N、E点;BE交AD于点M;DF交BC于点K.求证:AF=CE.
如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF分别交BE、BC、DF于G、P、F点;CE分别交DF、AD、BE于H、N、E点;BE交AD于点M;DF交BC于点K.求证:AF=CE.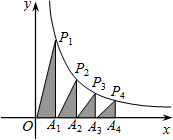 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3…=A2014A2015=1,过点A1、A2、A3、…、A2015分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、…P2015,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、…A2014P2015A2015,并设其面积分别为S1、S2、S3、…S2015,则S2015的值为$\frac{1}{2015}$.
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3…=A2014A2015=1,过点A1、A2、A3、…、A2015分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、…P2015,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、…A2014P2015A2015,并设其面积分别为S1、S2、S3、…S2015,则S2015的值为$\frac{1}{2015}$.