题目内容
7. 在△ABC中,∠B,∠C的角平分线相交于点O,过O作DE∥BC,交AB于D点,交AC于E点,若BD+EC=6,则DE等于( )
在△ABC中,∠B,∠C的角平分线相交于点O,过O作DE∥BC,交AB于D点,交AC于E点,若BD+EC=6,则DE等于( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 根据OB和OC分别平分∠ABC和∠ACB,和DE∥BC,利用两直线平行,内错角相等和等量代换,求证出DB=DO,OE=EC.然后即可得出答案.
解答 解:∵在△ABC中,OB和OC分别平分∠ABC和∠ACB,
∴∠DBO=∠OBC,∠ECO=∠OCB,
∵DE∥BC,
∴∠DOB=∠OBC=∠DBO,∠EOC=∠OCB=∠ECO,
∴DB=DO,OE=EC,
∵DE=DO+OE,
∴DE=BD+EC=6.
故选A.
点评 此题主要考查学生对等腰三角形的判定与性质平行线段性质的理解和掌握,此题关键是求证DB=DO,OE=EC,难度不大,是一道基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
15.在下列数:-3,0,1,-$\frac{1}{2}$中,属于负数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.月球到地球的距离约384000千米,它的长度用科学记数法表示为多少米?( )
| A. | 0.384×109 | B. | 3.84×108 | C. | 3.84×107 | D. | 3.84×105 |
12.下列二次根式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{27}$ |
19.下面给出的图形分别是直线,射线和线段,能相交的图形是( )


| A. | ①③ | B. | ①② | C. | ①④ | D. | ③④ |
17. 如图,设在点O的观测站测得渔船A、B的方向分别为北偏东50°、南偏西30°,为了减少相互干扰并取得好的捕鱼效益,渔船C恰好位于∠AOB的角平分线上,求渔船C相对观测站的方向.( )
如图,设在点O的观测站测得渔船A、B的方向分别为北偏东50°、南偏西30°,为了减少相互干扰并取得好的捕鱼效益,渔船C恰好位于∠AOB的角平分线上,求渔船C相对观测站的方向.( )
 如图,设在点O的观测站测得渔船A、B的方向分别为北偏东50°、南偏西30°,为了减少相互干扰并取得好的捕鱼效益,渔船C恰好位于∠AOB的角平分线上,求渔船C相对观测站的方向.( )
如图,设在点O的观测站测得渔船A、B的方向分别为北偏东50°、南偏西30°,为了减少相互干扰并取得好的捕鱼效益,渔船C恰好位于∠AOB的角平分线上,求渔船C相对观测站的方向.( )| A. | 南偏东50° | B. | 东偏南50° | C. | 东南方 | D. | 不能确定 |
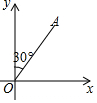 某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.
某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.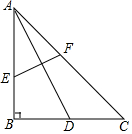 如图所示,在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,把A点翻折与点D重合,得到折痕EF,设AE=x,BE=y,求y与x之间的函数解析式.并写出函数定义域.
如图所示,在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,把A点翻折与点D重合,得到折痕EF,设AE=x,BE=y,求y与x之间的函数解析式.并写出函数定义域.