题目内容
16.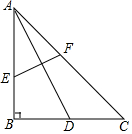 如图所示,在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,把A点翻折与点D重合,得到折痕EF,设AE=x,BE=y,求y与x之间的函数解析式.并写出函数定义域.
如图所示,在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,把A点翻折与点D重合,得到折痕EF,设AE=x,BE=y,求y与x之间的函数解析式.并写出函数定义域.
分析 连接ED,根据勾股定理列出方程,解方程求出x、y的关系,即可得到结论.再由题目已知条件即可确定函数定义域.
解答 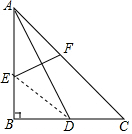 解:连接ED,
解:连接ED,
∵AE=x>0,BE=y>0,
∴AB=BC=x+y,
∵AD是BC边上的中线,
∴BD=$\frac{1}{2}$(x+y),
由翻转变换的性质可知,DE=AE=x,
由勾股定理得,x2=[$\frac{1}{2}$(x+y)]2+y2,
化简得:3x2-2xy-5y2=0,
∴(x+y)(3x-5y)=0,
解得,y=$\frac{3}{5}$x,y=-x(舍去).
∴y与x之间的函数解析式为:y=$\frac{3}{5}$x,(0<x<x+y).
点评 本题考查的是翻转变换的性质、勾股定理的应用,掌握翻转变换的性质、灵活运用方程思想是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
4.在-3.5,5,$\frac{22}{7}$,0,π,0.1010010001…中,有理数共有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
11.已知:(x+y)2=12,(x-y)2=4,则x2+3xy+y2的值为( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
1.在代数式$\frac{3}{a}$,$\frac{2x-3y}{5}$,$\frac{1}{3}$(m+n),$\frac{x+y}{x-y}$,$\frac{8}{x-1}$中,分式个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.点A,B,C在同一条直线上,已知AB=5,BC=3,则线段AC=( )
| A. | 8 | B. | 2 | C. | 8或2 | D. | 无法确定 |
5.已知x>y,a为任意实数,则下列式子成立的是( )
| A. | -x>-y | B. | -2x<-2y | C. | x-1<y-1 | D. | a2x>a2y |
6.下列方程是二元一次方程的是( )
| A. | xy+5=4 | B. | x+y=1 | C. | x2-y=3 | D. | x+$\frac{1}{y}$=2 |
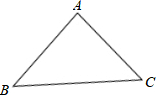 已知等腰Rt△ABC,∠BAC=90°,D为平面内 一点,∠ADC=45°,AD=2$\sqrt{2}$,CD=3,求BD的长.
已知等腰Rt△ABC,∠BAC=90°,D为平面内 一点,∠ADC=45°,AD=2$\sqrt{2}$,CD=3,求BD的长. 在△ABC中,∠B,∠C的角平分线相交于点O,过O作DE∥BC,交AB于D点,交AC于E点,若BD+EC=6,则DE等于( )
在△ABC中,∠B,∠C的角平分线相交于点O,过O作DE∥BC,交AB于D点,交AC于E点,若BD+EC=6,则DE等于( )