题目内容
17.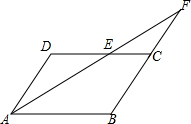 如图,?ABCD中,点E是CD边的中点,连接AE并延长交BC延长线于点F.
如图,?ABCD中,点E是CD边的中点,连接AE并延长交BC延长线于点F.(1)求证:△ADE≌△FCE;
(2)若AE平分∠BAD,连接BE,猜想BE与AF的位置关系,并说明理由.
分析 (1)由平行四边形的性质得出∠D=∠ECF,根据ASA即可判定△ADE≌△FCE;
(2)先证明AD=DE,得出AB=2AD,再由△ADE≌△FCE,得出AE=FE,AD=CF,得出BF=AB,根据等腰三角形的三线合一性质即可得出结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴∠D=∠ECF,
∵点E是CD边的中点,
∴DE=CE,
在△ADE和△FCE中,
$\left\{\begin{array}{l}{∠D=∠ECF}&{\;}\\{DE=CE}&{\;}\\{∠AED=∠FEC}&{\;}\end{array}\right.$,
∴△ADE≌△FCE(ASA);
(2)解:BE⊥AF,理由如下:
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∵AB∥CD,
∴∠DEA=∠BAE,
∴∠DAE=∠DEA,
∴AD=DE,
∴BC=AD=DE,AB=2AD,
由(1)得:△ADE≌△FCE,
∴AE=FE,AD=CF,
∴BF=2AD=AB,
∴BE⊥AF(三线合一).
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
6.为了了解500名初三毕业班学生一分钟跳绳次数的情况,某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试,将所得数据进行处理,可得频率分布表:
(1)这个问题中,总体是初三毕业班学生一分钟跳绳次数的情况的全体;样本容量a=100;
(2)第四小组的频数b=39,频率c=0.39;
(3)若次数在110次(含110次)以上为达标,试估计该校初三毕业生一分钟跳绳的达标率是多少?
| 组别 | 分组 | 频数 | 频率 |
| 1 | 89.5~99.5 | 4 | 0.04 |
| 2 | 99.5~109.5 | 3 | 0.03 |
| 3 | 109.5~119.5 | 46 | 0.46 |
| 4 | 119.5~129.5 | B | c |
| 5 | 129.5~139.5 | 6 | 0.06 |
| 6 | 139.5~149.5 | 2 | 0.02 |
| 合计 | a | 1.00 | |
(2)第四小组的频数b=39,频率c=0.39;
(3)若次数在110次(含110次)以上为达标,试估计该校初三毕业生一分钟跳绳的达标率是多少?
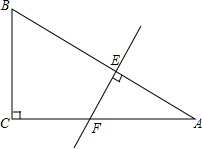 如图,在△ABC中,∠C=90°,∠A=22.5°,AB的垂直平分线交AC于F,交AB于E,若CF=3cm,求BC的长.
如图,在△ABC中,∠C=90°,∠A=22.5°,AB的垂直平分线交AC于F,交AB于E,若CF=3cm,求BC的长.