题目内容
5.为了解某市初中学生每天进行体育锻炼的时间,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.| 类别 | 时间t(小时) | 人数 |
| A | t≤0.5 | 5 |
| B | 0.5<t≤1 | m |
| C | 1<t≤1.5 | n |
| D | 1.5<t≤2 | 30 |
| E | t>2 | 10 |
 ①
①请根据图表信息解答下列问题:
(1)在统计表中,m=20,n=35,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是126°;
(3)据了解该市大约有3万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
分析 (1)用总人数乘以B类别百分比可得m的值,用总人数减去A、B、D、E的人数可得C类别人数,补全条形统计图;
(2)用C类别人数占总人数的比例乘以360°即可;
(3)用每天进行体育锻炼时间在1小时以上的人数占总人数的比例乘以总体中学生总数即可.
解答 解:(1)m=100×20%=20,n=100-5-20-30-10=35,补全图形如下:
故答案为:20,35;
(2)扇形统计图中“C组”所对应的圆心角的度数是$\frac{35}{100}$×360°=126°,
故答案为:126°.
(3)30000×$\frac{35+30+10}{100}$=22500(人),
答:估计该市初中学生每天进行体育锻炼时间在1小时以上的有22500人.
点评 本题考查的是条形统计图和频数分布表的综合运用.读懂统计图表,从不同的统计图表中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.也考查了利用样本估计总体.

练习册系列答案
相关题目
15.下列方程中有两个不相等实数根的方程是( )
| A. | x2-2$\sqrt{2}$x+2=0 | B. | $\sqrt{{x}^{2}-2}$=-1 | C. | x2-3x+4=0 | D. | 2x2-7x+2=0 |
13.如果盈利20元记作+20,那么亏本50元记作( )
| A. | +50元 | B. | -50元 | C. | +20元 | D. | -20元 |
10.八年级学生去距学校11km的科技馆参观,一部分学生骑自行车,过了20min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度,设骑车学生的速度为xkm/h,则所列方程正确的是( )
| A. | $\frac{11}{x}=\frac{11}{2x}-\frac{1}{3}$ | B. | $\frac{11}{x}=\frac{11}{2x}-20$ | C. | $\frac{11}{x}=\frac{11}{2x}+\frac{1}{3}$ | D. | $\frac{11}{x}=\frac{11}{2x}+20$ |
14. 今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
(1)B种树苗成活了多少棵?并补全条形统计图;
(2)若明年B种树苗要成活3000棵,则今年植树节需种B种树苗至少几棵?
 今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.(1)B种树苗成活了多少棵?并补全条形统计图;
(2)若明年B种树苗要成活3000棵,则今年植树节需种B种树苗至少几棵?
| 品种 | 今年成活棵树 | 成活率 |
| A | 540 | 90% |
| B | a | 96% |
| C | 368 | 92% |
| 合计 | 1388 |
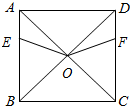 已知正方形ABCD,AB=8,点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t.
已知正方形ABCD,AB=8,点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t.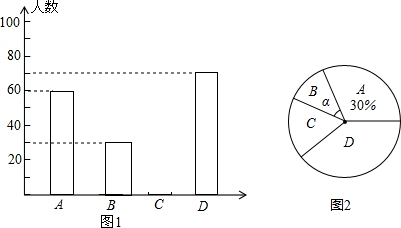 黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题: