下列方程中有两个不相等实数根的方程是( )A．x2-2$\sqrt{2}$x+2=0B．$\sqrt{{x}^{2}-2}$=-1C．x2-3x+4=0D．2x2-7x+2=0 题目和参考答案——青夏教育精英家教网——

题目内容

15．下列方程中有两个不相等实数根的方程是（　　）

A．

x²-2$\sqrt{2}$x+2=0

B．

$\sqrt{{x}^{2}-2}$=-1

C．

x²-3x+4=0

D．

2x²-7x+2=0

分析根据一元二次方程根的判别式，分别计算△的值，根据△＞0，方程有两个不相等的实数根；△=0，方程有两个相等的实数根；△＜0，方程没有实数根，进行判断．

解答解：A、△=0，方程有两个相等实数根；
B、方程是无理方程；
C、△=9-16=-7＜0，方程没有实数根；
D、△=49-16＞0，方程有两个不相等的实数根．
故选D．

点评本题考查了无理方程以及根的判别式，利用一元二次方程的根的判别式判定方程的根的情况是解题的关键．

练习册系列答案

Happy holiday欢乐假期暑假作业广东人民出版社系列答案

状元龙快乐学习暑假在线北方妇女儿童出版社系列答案

开拓者系列丛书高中新课标假期作业暑假作业内蒙古人民出版社系列答案

金牛系列高中新课标假期作业暑大众文艺出版社系列答案

石室金匮暑假作业电子科技大学出版社系列答案

学与练暑假生活宁夏人民教育出版社系列答案

优等生暑假作业云南人民出版社系列答案

快乐暑假暑假能力自测中西书局系列答案

志诚教育假期园地暑假作业中原农民出版社系列答案

快乐练习暑假衔接优计划晨光出版社系列答案

相关题目

5．解下列方程组
（1）$\left\{\begin{array}{l}{2x-y=5}\\{7x-3y=20}\end{array}\right.$
（2）$\left\{\begin{array}{l}{\frac{x+3y}{2}=\frac{3}{5}}\\{5（x-2y）=-4}\end{array}\right.$．

6．某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度，抽取部分学生进行调查，被调查的每个学生按A（非常喜欢）、B（比较喜欢）、C（一般）、D（不喜欢）四个等级对活动评价，图（1）和图（2）是该小组采集数据后绘制的两幅统计图，经确认扇形统计图是正确的，而条形统计图尚有一处错误且并不完整．请你根据统计图提供的信息，解答下列问题：

（1）此次调查的学生人数为200；
（2）条形统计图中存在错误的是C（填A，B，C，D中的一个），人数应改为50；
（3）补画图2中条形统计图中不完整的部分；
（4）如果该校有6000名学生，那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人？

3．估计$\sqrt{50}$-5的值是（　　）

10．计算：$\sqrt{64}$+$\root{3}{-64}$-$\sqrt{\frac{1}{4}}$．

20．若关于x的方程kx²-4x-1=0有实数根，则k的取值范围是k≥4．

7．2016年举国县教育部确定为全国中小学研究旅行实验区，成为江西省唯一获得此项荣誉的地区，某校准备从A---将军园、B---官田兵工厂、C---长冈乡调查纪念馆、D---潋江书院四个红色基地中选择安排一个作为县内研究学旅行地点，为了解学生的兴趣，对八年级某班同学的选择情况进行调查统计，制成了两幅不完整的统计图（如图）

（1）请你求出该班的总人数；
（2）把条形统计图补充完整；
（3）某型客车座位数为35，若该校八年级共有500名学生，根据抽样调查结果，请估计至少要安排几辆该型号客车去将军园？

4．（1）计算：$\sqrt{0.04}$+$\root{3}{8}$-$\sqrt{\frac{1}{4}}$+|$\sqrt{3}$-2|+3$\sqrt{3}$
（2）说出下列数轴上A，B，C，D，E，F各点所对应的下列实数：-1-$\sqrt{2}$，$\sqrt{3}$，$\sqrt{5}$，-$\sqrt{10}$，π

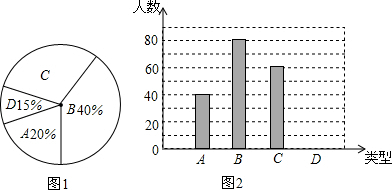
5．为了解某市初中学生每天进行体育锻炼的时间，随机抽样调查了100名初中学生，根据调查结果得到如图所示的统计图表．

类别	时间t（小时）	人数
A	t≤0.5	5
B	0.5＜t≤1	m
C	1＜t≤1.5	n
D	1.5＜t≤2	30
E	t＞2	10

①
请根据图表信息解答下列问题：
（1）在统计表中，m=20，n=35，并补全条形统计图；
（2）扇形统计图中“C组”所对应的圆心角的度数是126°；
（3）据了解该市大约有3万名初中学生，请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数．