题目内容
17. 如图,已知AB是⊙O的直径,C是圆上一点,延长BC至D,使CD=BC,连接AD,过C作CE⊥AD于E,BE交⊙O于F.求证:EF•EB=AE•DE.
如图,已知AB是⊙O的直径,C是圆上一点,延长BC至D,使CD=BC,连接AD,过C作CE⊥AD于E,BE交⊙O于F.求证:EF•EB=AE•DE.
分析 由于AB是⊙O的直径,考虑连接AC,得直角三角形.在直角三角形中,因为CE⊥AD于E,满足射影定理,
CE2=DE•AE,证明CE2=EF•EB是关键,所以考虑切割线定理,解决问题需证明CE是切线,利用BC=CD及半径长相等得证.
解答 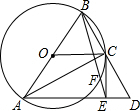 证明:连接AC、OC
证明:连接AC、OC
∵AB是直径,∴∠BCA=90°=∠ACD,AC⊥BD.
在Rt△ACD中,∵CE⊥AD于E,
∴CE2=DE•AE(射影定理)
∵AC⊥BD,BC=CD,
∴∠BAC=∠CAD(三线合一),
∵OC=OA,
∴∠OCA=∠OAC=∠CAD,
∴OC∥AD.
∴∠OCE=∠AEC=90°,
因为点C在⊙O上,∠OCE=90°,
∴CE是⊙O的切线,
∴CE2=EF•EB(切割线定理)
∴EF•EB=AE•DE.
点评 本题考查了圆的有关性质及切割线定理、射影定理等.也可通过证明三角形相似得到结?论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.在$-\frac{3}{4}$,$-\frac{4}{5}$,$-\frac{5}{6}$,$-\frac{6}{7}$这四个数中,最小的数是( )
| A. | $-\frac{6}{7}$ | B. | $-\frac{5}{6}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{4}$ |
8.某等腰三角形的周长等于16cm,一边长为4cm,则另一边长为( )
| A. | 5cm | B. | 6cm | C. | 8cm | D. | 6cm或8cm |
9.计算$\sqrt{12}$+3$\sqrt{1\frac{1}{3}}$-$\sqrt{5\frac{1}{3}}$-$\frac{2}{3}$$\sqrt{48}$,得( )
| A. | 1$\frac{1}{3}$ | B. | 0 | C. | $\frac{16}{3}$$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
6.矩形中,对角线把矩形的一个直角分成1:2两部分,则矩形对角线所夹的锐角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |

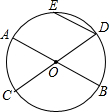 如图所示,AB、CD为⊙O的两条直径,E是圆上一点,连接DE,如果DE∥AB,$\widehat{DE}$=$\widehat{AE}$,则∠BOC的度数为120°.
如图所示,AB、CD为⊙O的两条直径,E是圆上一点,连接DE,如果DE∥AB,$\widehat{DE}$=$\widehat{AE}$,则∠BOC的度数为120°.