题目内容
计算:3(a-b)2•[9(a-b)n+2]•(b-a)5= .
考点:单项式乘单项式
专题:
分析:化为同底数幂,再根据单项式乘单项式计算即可.
解答:解:原式=3(a-b)2•[9(a-b)n+2]•[-(a-b)5]
=-27(a-b)2+n+2+5
=-27(a-b)n+9,
故答案为:-27(a-b)n+9
=-27(a-b)2+n+2+5
=-27(a-b)n+9,
故答案为:-27(a-b)n+9
点评:本题主要考查了单项式乘单项式,熟练掌握运算法则是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题中是真命题的是( )
| A、如果a2=b2,那么a=b |
| B、对角线互相垂直的四边形是菱形 |
| C、多边形的内角和等于360° |
| D、全等三角形的面积相等 |
 如图,已知矩形ABCD的四个顶点都在圆O上,且
如图,已知矩形ABCD的四个顶点都在圆O上,且
 如图,AB∥CD,E为AD上一点,且BE、CE分别平分∠ABC、∠BCD,求证:AE=ED.
如图,AB∥CD,E为AD上一点,且BE、CE分别平分∠ABC、∠BCD,求证:AE=ED.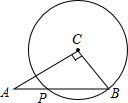 如图,Rt△ABC中,∠C=90°,AC=
如图,Rt△ABC中,∠C=90°,AC=