Question

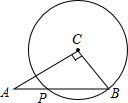如图，Rt△ABC中，∠C=90°，AC=

3

，BC=1，若以点C为圆心，CB为半径的圆交AB点P，则AP=

 

．

Answer 1

考点：垂径定理,勾股定理

专题：

分析：延长AC交⊙C与E，设与圆的另一个交点为Q，首先在Rt△ABC中利用勾股定理即可求出AB的长度，根据题意可以知道CQ=CB=CE=1，然后根据相交弦定理即可求出AP的长度．

解答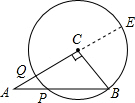：解：如图，延长AC交⊙C与E，设与圆的另一个交点为Q，
在Rt△ABC中，
∵∠C=90°，AC=

3

，BC=1，
∴AB=

AC2+BC2

=

( 3 )2+12

=2．
∵CQ、CB、CE都是圆的半径，
∴CQ=CB=CE=1，
根据相交弦定理得AQ•AE=AP•AB，
∴AP=

AQ•AE

AB

=

( 3 -1)•( 3 +1)

2

=1．
故答案为：1．

点评：本题考查的是勾股定理及相交弦定理，根据题意作出辅助线，构造出相交弦是解答此题的关键．