题目内容
15.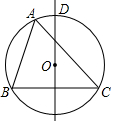 如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )
如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )| A. | 23° | B. | 28° | C. | 30° | D. | 37° |
分析 首先连接OB,OC,AO,设DO交BC于点E,由∠B=74°,∠C=46°,即可求得∠BAC的度数,又由△ABC的边BC的垂直平分线与△ABC的外接圆相交于点D,根据圆周角定理,即可求得∠AOB与∠BOE的度数,继而求得答案.
解答 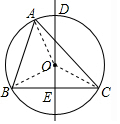 解:如图,连接OB,OC,AO,设DO交BC于点E,
解:如图,连接OB,OC,AO,设DO交BC于点E,
∵OD是△ABC的边BC的垂直平分线,
∴∠BOE=$\frac{1}{2}$∠BOC,
∵∠BAC=$\frac{1}{2}$∠BOC,
∴∠BOE=∠BAC,
∵∠ABC=74°,∠ACB=46°,
∴∠BOE=∠BAC=180°-∠ABC-∠ACB=60°,
∴∠BOD=180°-∠BOE=180°-60°=120°,
∵∠AOB=2∠ACB=92°,∴$\widehat{AB}$的度数为:92°,
∴$\widehat{AD}$的度数为:120°-92°=28°.
故选:B.
点评 此题考查了圆周角定理以及线段垂直平分线的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
3.一个各面分别标有数字1,2,3,4,5,6的骰子,连续投掷二次,分别出现数字m,n,得到一个点P(m,n),则点P既在直线y=-x+5上,又在双曲线y=$\frac{6}{x}$上的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{36}$ |
10.若2y-3x=0,则x:y的值等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $-\frac{3}{2}$ | D. | $-\frac{2}{3}$ |
7.下列各数中,是负数的是( )
| A. | -(-3) | B. | -|-3| | C. | |+3| | D. | |-3| |
4.某商店为吸引顾客设计了促销活动:在一不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客一次性消费满400元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回),某顾客刚好消费400元,则该顾客获得的金额不低于30元的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
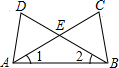 如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中正确的有( )
如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中正确的有( )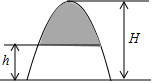 如图所示的图形,是由开口向下的抛物线两边平齐的一部分和一水平线段围成的,设其总高度为H,空白部分的高度是h(0≤h≤H),阴影部分的面积是S,则S随h变化的大致趋势是( )
如图所示的图形,是由开口向下的抛物线两边平齐的一部分和一水平线段围成的,设其总高度为H,空白部分的高度是h(0≤h≤H),阴影部分的面积是S,则S随h变化的大致趋势是( )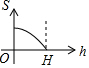
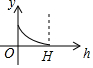
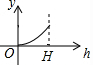
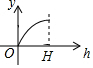

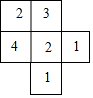 如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面看和从上面看到的图形(要用直尺画).
如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面看和从上面看到的图形(要用直尺画).