题目内容
19.一名射击爱好者在一次射击测试中,前9次射击的平均环数为8环(9次射击命中的环数不全相等),他第10次射击的环数也为8环,则该射击爱好者前9次射击的稳定性与这10次射击的稳定性之间的关系为( )| A. | 一样稳定 | B. | 前者比后者稳定 | C. | 后者比前者稳定 | D. | 无法确定 |
分析 根据方差的计算公式可得出前9次射击的稳定性没有前10次射击环数的稳定性.
解答 解:设前9次射击的方差为${{S}_{1}}^{2}$,前10次射击环数的方差为${{S}_{2}}^{2}$,
∵前9次射击环数的平均数与前10次射击环数的平均数相等,
∴前9次射击的方差为大于前10次射击环数的方差,
即${{S}_{1}}^{2}$>${{S}_{2}}^{2}$,
∴后者比前者稳定,
故选C.
点评 本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.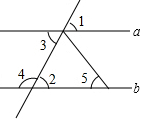 如图,在下列条件中,不能判定直线a与b平行的是( )
如图,在下列条件中,不能判定直线a与b平行的是( )
 如图,在下列条件中,不能判定直线a与b平行的是( )
如图,在下列条件中,不能判定直线a与b平行的是( )| A. | ∠1=∠2 | B. | ∠2=∠3 | C. | ∠3+∠4=180° | D. | ∠3=∠5 |
7.某区的绿化覆盖率由如下统计数据:
如果以后的几年继续依此速度发展绿化.
(1)观察此表格,第5年年底的绿化覆盖率为多少?
(2)探索规律,问第10年年底的绿化覆盖率为多少?第n年年底的绿化覆盖率为多少?﹙n≤35的正整数﹚
| 年份 | 第1年年底 | 第2年年底 | 第3年年底 | 第4年年底 |
| 绿化覆盖率﹙%﹚ | 22.2 | 23.8 | 25.4 | 27.0 |
| 年份 | 第5年年底 | … | 第10年年底 | |
| 绿化覆盖率﹙%﹚ |
(1)观察此表格,第5年年底的绿化覆盖率为多少?
(2)探索规律,问第10年年底的绿化覆盖率为多少?第n年年底的绿化覆盖率为多少?﹙n≤35的正整数﹚
