题目内容
18.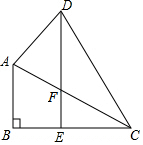 如图,在四边形ABCD中,∠B=90°,DE∥AB交BC于E、交AC于F,∠CDE=∠ACB=30°,BC=DE.求证:△FCD是等腰三角形.
如图,在四边形ABCD中,∠B=90°,DE∥AB交BC于E、交AC于F,∠CDE=∠ACB=30°,BC=DE.求证:△FCD是等腰三角形.
分析 由平行可求得∠EFC,由三角形的外角可求得∠FCD,则可证明FD=FC,可证得结论.
解答 证明:
∵∠B=90°,∠ACB=30°,
∴∠BAC=60°
∵AB∥DE,
∴∠EFC=∠BAC=60°,
∵∠CDE=30°,
∴∠FCD=∠EFC-∠CDE=60°-30°=30°,
∴∠FCD=∠FDC,
∴FD=FC,即△FCD为等腰三角形.
点评 本题主要考查等腰三角形的判定,利用条件求得∠FCD的度数是解题的关键,注意三角形外角性质的应用.

练习册系列答案
相关题目
6.若(a-3)2+|b-4|=0,则(a-b)2004的值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2016 |
10. 如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
 如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 无法确定 |
6. 如图,一个螺母的实物图,它的俯视图应该是( )
如图,一个螺母的实物图,它的俯视图应该是( )
 如图,一个螺母的实物图,它的俯视图应该是( )
如图,一个螺母的实物图,它的俯视图应该是( )| A. |  | B. |  | C. |  | D. |  |
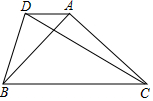 如图,在△ABC中,∠BAC=90°,AB=AC,DA∥BC,tan∠DBA=$\frac{1}{2}$,若CD=2$\sqrt{17}$,则线段BC的长为,6$\sqrt{2}$.
如图,在△ABC中,∠BAC=90°,AB=AC,DA∥BC,tan∠DBA=$\frac{1}{2}$,若CD=2$\sqrt{17}$,则线段BC的长为,6$\sqrt{2}$.
 如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.
如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.