题目内容
13. 如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙O上的一个动点,线段DA与y轴交于点E,则△ABE面积的最大值为( )
如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙O上的一个动点,线段DA与y轴交于点E,则△ABE面积的最大值为( )| A. | 2+$\sqrt{2}$ | B. | 2+$\frac{\sqrt{2}}{2}$ | C. | 1 | D. | 2 |
分析 由题意可得当AD和⊙C相切时,△ABE的面积最大,画出此时的图形,然后由已知条件和三角形的相似,可以求得此时的△ABE面积的最大值.
解答 解:由题意可得,当AD与⊙C相切时,△ABE的面积最大,此时点D在D1的位置,如下图所示,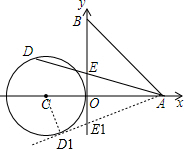
连接CD1,则∠CD1A=90°,
∴△CD1A∽△OE1A,
∴$\frac{OA}{{D}_{1}A}=\frac{O{E}_{1}}{{D}_{1}C}$
∵OA=2,AC=3,CD1=1,
∴$A{D}_{1}=\sqrt{{3}^{2}-{1}^{2}}=2\sqrt{2}$,
∴$O{E}_{1}=\frac{\sqrt{2}}{2}$,
∴${S}_{△AB{E}_{1}}=\frac{(2+\frac{\sqrt{2}}{2})×2}{2}$=2+$\frac{\sqrt{2}}{2}$,
故选B.
点评 本题考查切线的性质、一次函数图象上点的坐标特征、三角形的相似、最值,解题的关键是明确题意画出相应的图形,求出相应的图形的面积.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
3.已知点P关于y轴的对称点P1的坐标是(2,3),那么点P关于x轴的对称点P2的坐标为( )
| A. | (-3,-2) | B. | (-2,3) | C. | (-2,-3) | D. | (2,-3) |
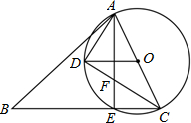 如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC. 在△ABC中,∠BAE是△ABC外角,AD是△ABC的外角平分线,∠BAC=∠BDC,求证:DB=DC.
在△ABC中,∠BAE是△ABC外角,AD是△ABC的外角平分线,∠BAC=∠BDC,求证:DB=DC. 如图,一直动点A在函数$y=\frac{4}{x}(x>0)$的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交于x轴于点P、Q,当$\frac{QE}{DP}=\frac{4}{9}$时,图中阴影部分的面积等于$\frac{13}{3}$.
如图,一直动点A在函数$y=\frac{4}{x}(x>0)$的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交于x轴于点P、Q,当$\frac{QE}{DP}=\frac{4}{9}$时,图中阴影部分的面积等于$\frac{13}{3}$. 已知△CDE是△CAB经相似变换后得到的像,且∠A=30°,∠CDE=30°,AB=4,DE=2,AC=3,则CD=1.5.
已知△CDE是△CAB经相似变换后得到的像,且∠A=30°,∠CDE=30°,AB=4,DE=2,AC=3,则CD=1.5. 如图,直线y=2(x-2)+n经过原点,与双曲线$y=\frac{n}{x}$相交与点A、B,过点A作AC垂直于x轴,过点B作BC垂直于y轴,AC与BC相交于点C.求:
如图,直线y=2(x-2)+n经过原点,与双曲线$y=\frac{n}{x}$相交与点A、B,过点A作AC垂直于x轴,过点B作BC垂直于y轴,AC与BC相交于点C.求: