题目内容
3. 掷两枚均匀的骰子,得到两个点数.
掷两枚均匀的骰子,得到两个点数.(1)在下面树形图中的括号内填写适当的数或结果;
(2)求两个点数的和是奇数的概率;
(3)求两个点数的和是偶数的概率.
分析 (1)画树状图展示4种等可能的结果数;
(2)根据概率公式求解;
(3)根据概率公式求解.
解答 解:(1)如图,
(2)两个点数的和是奇数的概率=$\frac{1}{4}$+$\frac{1}{4}$=$\frac{1}{2}$;
(3)两个点数的和是偶数的概率=$\frac{1}{4}$+$\frac{1}{4}$=$\frac{1}{2}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
相关题目
11.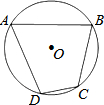 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )
 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )| A. | 64° | B. | 90° | C. | 136° | D. | 116° |
18.有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
(1)20筐白菜中,最重的一筐比最轻的一筐重5.5千克.
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这20筐白菜可卖多少元?
| 与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这20筐白菜可卖多少元?
15.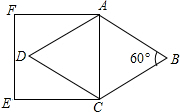 如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )
如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )
 如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )
如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )| A. | a>b | B. | a<b | C. | a=b | D. | 无法确定 |
12.抛物线y=$\frac{1}{2}$x2,y=-2x2,y=$\frac{2}{3}$x2共有的性质是( )
| A. | 开口向下 | B. | 对称轴是y轴 | ||
| C. | 都有最低点 | D. | y随x的增大而减小 |
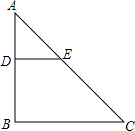 如图,DE∥BC,DB=AE,若AB=4,AC=5,求AE的长.
如图,DE∥BC,DB=AE,若AB=4,AC=5,求AE的长. 如图所示,将网络中△ABC绕点P逆时针旋转90°,得△A′B′C′,画出△A′B′C′.
如图所示,将网络中△ABC绕点P逆时针旋转90°,得△A′B′C′,画出△A′B′C′. 如图,△ABC的三个顶点郡在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,且点A′,C′仍落在格点上,则线段A′B的长是$\sqrt{13}$.
如图,△ABC的三个顶点郡在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,且点A′,C′仍落在格点上,则线段A′B的长是$\sqrt{13}$.