题目内容
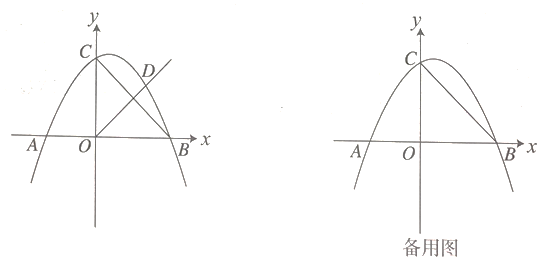
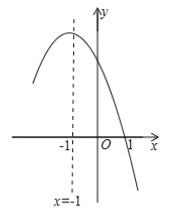
【题目】抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,且过点
,且过点![]() ,顶点位于第二象限,其部分图象如图所示,给出以下判断;①
,顶点位于第二象限,其部分图象如图所示,给出以下判断;①![]() 且
且![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤直线
;⑤直线![]() 与抛物线
与抛物线![]() 两个交点的横坐标分别为
两个交点的横坐标分别为![]() ,则
,则![]() .其中结论正确是___________.
.其中结论正确是___________.
【答案】②④⑤
【解析】
根据题意得到a、b、c的关系式,可以用a表示出b、c,进而得到含a的二次函数关系式,结合图像确定符号,对选项逐一判断即可.
解:∵抛物线的对称轴为直线![]() ,
,
∴![]() ,即
,即![]() .
.
又∵抛物线经过点![]() ,
,
∴![]() ,∴
,∴![]() .
.
∴抛物线的解析式亦可表示为![]() .
.
由图,抛物线开口向下,则![]() .
.
∴![]() ,
,![]() ,
,
∴①错误;
由抛物线的对称性知,抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() ,
,
因此,当自变量![]() 时,函数值
时,函数值![]() ,
,
∴②正确;
![]() ,∵
,∵![]() ,所∴
,所∴![]() ,
,
即![]() ,
,
∴③错误;
![]() ,而
,而![]() ,
,
∴![]() ,
,
∴④正确;
联立解析式:![]() ,
,
即![]() ,
,
得![]()
![]() ,
,
∴![]() ,
,
∴⑤正确.
故答案为:②④⑤

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 |
|
|
| … |
我们把某格中字母和所得到的多项式称为特征多项式,例如:
第1格的“特征多项式”为![]() ;
;
第2格的“特征多项式”为![]() .
.
回答下列问题:
(1)第3格的“特征多项式”为________________,
第4格的“特征多项式”为______________________,
第![]() 格的“特征多项式”为___________________;
格的“特征多项式”为___________________;
(2)若第1格的“特征多项式”的值为![]() ,第2格的“特征多项式”的值为
,第2格的“特征多项式”的值为![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,第![]() 格的特征多项式的值为
格的特征多项式的值为![]() ,则直接写出
,则直接写出![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.