题目内容
20. 如图,在Rt△ABC中,∠BAC=90°,如果∠A=30°,D为AB的中点,BC=3cm,则CD=3cm.
如图,在Rt△ABC中,∠BAC=90°,如果∠A=30°,D为AB的中点,BC=3cm,则CD=3cm.
分析 根据含30°角的直角三角形性质求出AB,根据直角三角形斜边上中线性质求出CD即可.
解答 解:∵在Rt△ABC中,∠BAC=90°,∠A=30°,BC=3cm,
∴AB=2BC=6cm,
∵D为AB的中点,
∴CD=$\frac{1}{2}$AB=3cm,
故答案为:3cm.
点评 本题考查了含30°角的直角三角形性质,直角三角形斜边上中线性质的应用,能根据性质求出AB=2BC和CD=$\frac{1}{2}$AB是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.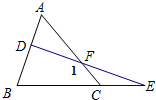 如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )
如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )
 如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )
如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )| A. | ∠A+∠B=∠1+∠E | B. | ∠A+∠B=∠1-∠E | C. | ∠A-∠B=∠1-∠E | D. | ∠A-∠B=∠1+∠E |
12.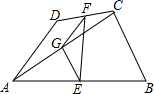 如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )
如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )
 如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )
如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )| A. | 20° | B. | 24° | C. | 26° | D. | 15° |
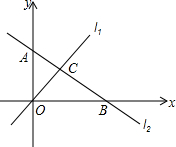 如图,直线l1:y=2x和直线l2:y=kx+b交于C点,A(0,2),B(4,0).
如图,直线l1:y=2x和直线l2:y=kx+b交于C点,A(0,2),B(4,0).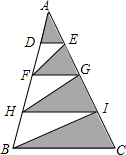 如图,三角形ABC中,将AB,AC分别四等分,已知三角形ADE的面积是6cm2,求阴影部分的面积.
如图,三角形ABC中,将AB,AC分别四等分,已知三角形ADE的面积是6cm2,求阴影部分的面积.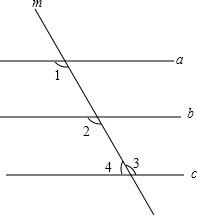 如图,直线a,b,c被直线m所截,量得∠1=∠2=∠3.
如图,直线a,b,c被直线m所截,量得∠1=∠2=∠3.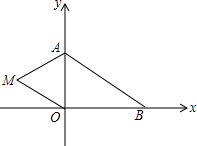 如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.
如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.