题目内容
20．
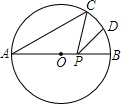如图，AB是⊙O的直径，AB=4，点C在⊙O上，∠CAB=30°，D为$\widehat{BC}$的中点，P是直径AB上一动点，则PC+PD的最小值为（ ）| A． | 2$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | 1 | D． | 2 |
分析 作出D关于AB的对称点D′，则PC+PD的最小值就是CD′的长度，在△COD′中根据边角关系即可求解．
解答 解：作出D关于AB的对称点D′，连接OC，OD′，CD′．
又∵点C在⊙O上，∠CAB=30°，D为$\widehat{BC}$的中点，
∴∠BAD′=$\frac{1}{2}$∠CAB=15°．
∴∠CAD′=45°．
∴∠COD′=90°．则△COD′是等腰直角三角形．
∵OC=OD′=$\frac{1}{2}$AB=2，
∴CD′=2$\sqrt{2}$，
故选：A．
点评 本题考查了圆周角定理以及路程的和最小的问题，正确作出辅助线是解题的关键．
练习册系列答案
相关题目
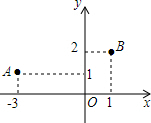如图，在平面直角坐标系中点A（-3，1），点B（1，2），一束光线从点A处沿直线射出经x轴反射后，正好经过点B，则光线从A到B所经过路程为5．
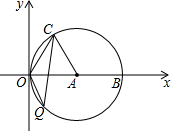如图，在平面直角坐标系xOy中，点A的坐标为（4，0），以点A为圆心，4为半径的圆与x轴交于O，B两点，OC为弦，∠AOC=60°，当点P在直径OB上运动时，连CP并延长与⊙A相交于点Q，PO=2或2+2$\sqrt{3}$时，△OCQ是等腰三角形．
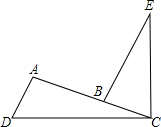已知∠DCE=90°，∠DAC=90°，BE⊥AC于B，且DC=EC，则与AB+AD相等的线段是BE和AC．
如图，在Rt△ABC中，∠BAC的平分线交BC于点D，E为AB上一点，DE=DC，以D为圆心，DB为半径作⊙D．求证：
已知在平面直角坐标系xOy中（如图），抛物线y=ax2-4与x轴的负半轴相交于点A，与y轴相交于点B，AB=$2\sqrt{5}$．点P在抛物线上，线段AP与y轴的正半轴交于点C，线段BP与x轴相交于点D．设点P的横坐标为m．