题目内容
1．
如图，Rt△ABC中，∠C=90°，sinB=$\frac{4}{5}$，AB=10．则tanA=$\frac{3}{4}$．
分析 先根据勾股定理得出BC的长，再由嘴角三角函数的定义即可得出结论．
解答 解：∵Rt△ABC中，∠C=90°，sinB=$\frac{4}{5}$，AB=10，
∴$\frac{AC}{AB}$=$\frac{4}{5}$=$\frac{AC}{10}$，
∴AC=8，
∴BC=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∴tanA=$\frac{BC}{AC}$=$\frac{6}{8}$=$\frac{3}{4}$．
故答案为：$\frac{3}{4}$．
点评 本题考查的是互余两角三角函数关系，熟记锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
如图，海中有一个小岛A，轮船在B点测得小岛A在北偏东45°方向上，轮船由西向东航行20海里到达D点，这时测得小岛A在北偏东30°方向上，求此时轮船与小岛A的距离AD是多少海里？（结果精确到0.1）参考数值：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732．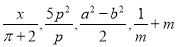
，其中分式共有（ ）．
， 
，为了发展经济，甲、乙两村准备合建一个工厂．经协商，工厂必须满足以下两个要求：