ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ![]() ≥«”–Ζ Νœ
≥«”–Ζ Νœ![]() Θ§
Θ§![]() ≥«”–Ζ Νœ
≥«”–Ζ Νœ![]() .œ÷“ΣΑ―’β–©Ζ Νœ»Ϊ≤Ω‘ΥΆυ
.œ÷“ΣΑ―’β–©Ζ Νœ»Ϊ≤Ω‘ΥΆυ![]() ΓΔ
ΓΔ![]() ΝΫœγΘ§
ΝΫœγΘ§![]() œγ–η“ΣΖ Νœ240tΘ§
œγ–η“ΣΖ Νœ240tΘ§![]() œγ–η“ΣΖ Νœ
œγ–η“ΣΖ Νœ![]() Θ§Τδ‘ΥΆυ
Θ§Τδ‘ΥΆυ![]() ΓΔ
ΓΔ![]() ΝΫœγΒΡ‘ΥΖ―»γœ¬±μΘΚ
ΝΫœγΒΡ‘ΥΖ―»γœ¬±μΘΚ
ΝΫ≥«/ΝΫœγ | C/(‘Σ/ | D/(‘Σ/ |
| 20 | 24 |
| 15 | 17 |
…η¥”![]() ≥«‘ΥΆυ
≥«‘ΥΆυ![]() œγΒΡΖ ΝœΈΣ
œγΒΡΖ ΝœΈΣ![]() Θ§¥”
Θ§¥”![]() ≥«‘ΥΆυΝΫœγΒΡΉή‘ΥΖ―ΈΣ
≥«‘ΥΆυΝΫœγΒΡΉή‘ΥΖ―ΈΣ![]() ‘ΣΘ§¥”
‘ΣΘ§¥”![]() ≥«‘ΥΆυΝΫœγΒΡΉή‘ΥΖ―ΈΣ
≥«‘ΥΆυΝΫœγΒΡΉή‘ΥΖ―ΈΣ![]() ‘Σ
‘Σ
(1)Ζ÷±π–¥≥ω![]() ΓΔ
ΓΔ![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒ Ϋ(≤Μ“Σ«σ–¥Ή‘±δΝΩΒΡ»Γ÷ΒΖΕΈß)ΘΜ
÷°ΦδΒΡΚ· ΐΙΊœΒ Ϋ(≤Μ“Σ«σ–¥Ή‘±δΝΩΒΡ»Γ÷ΒΖΕΈß)ΘΜ
(2) ‘±»Ϋœ![]() ΓΔ
ΓΔ![]() ΝΫ≥«Ήή‘ΥΖ―ΒΡ¥σ–ΓΘΜ
ΝΫ≥«Ήή‘ΥΖ―ΒΡ¥σ–ΓΘΜ
(3)»τ![]() ≥«ΒΡΉή‘ΥΖ―≤ΜΒΟ≥§Ιΐ4800‘ΣΘ§‘θ―υΒς‘Υ ΙΝΫ≥«ΉήΖ―”ΟΒΡΚΆΉν…Ό?≤Δ«σ≥ωΉν–Γ÷ΒΘ°
≥«ΒΡΉή‘ΥΖ―≤ΜΒΟ≥§Ιΐ4800‘ΣΘ§‘θ―υΒς‘Υ ΙΝΫ≥«ΉήΖ―”ΟΒΡΚΆΉν…Ό?≤Δ«σ≥ωΉν–Γ÷ΒΘ°
ΓΨ¥πΑΗΓΩ![]() ΘΜ(2) Β±
ΘΜ(2) Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§![]() ≥«ΒΡΉή‘ΥΖ―Ϋœ…ΌΘΜΒ±
≥«ΒΡΉή‘ΥΖ―Ϋœ…ΌΘΜΒ±![]() ±Θ§
±Θ§![]() Θ§ΝΫ≥«ΒΡΉή‘ΥΖ―œύΒ»ΘΜΒ±
Θ§ΝΫ≥«ΒΡΉή‘ΥΖ―œύΒ»ΘΜΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§![]() ≥«ΒΡΉή‘ΥΖ―Ϋœ…ΌΘΜΘ®3Θ©Β±
≥«ΒΡΉή‘ΥΖ―Ϋœ…ΌΘΜΘ®3Θ©Β±![]() ±Θ§
±Θ§![]() ”–Ήν–Γ÷Β
”–Ήν–Γ÷Β![]()
ΓΨΫβΈωΓΩ
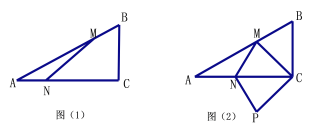
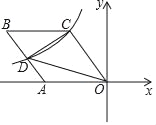
Θ®1Θ©ΗυΨίΧβΡΩΒΡ“Σ«σΘ§A≥«‘ΥΆυCœγΒΡΖ ΝœΈΣxtΘ§‘ρ‘ΥΆυDœγΒΡΖ ΝœΘ®200-xΘ©tΘ§¥”B≥«‘ΥΆυCœγΒΡΖ ΝœΈΣΘ®240-xΘ©tΘ§B≥«‘ΥΆυDœγΒΡΖ ΝœΈΣΘ®x+60Θ©t,¥ζ»κΦΤΥψΩ…ΒΟΒΫΫαΙϊΘ°
Θ®2Θ©”…Θ®1Θ©ΒΟΒΫΒΡ![]() Ϋχ––Ζ÷άύΧ÷¬έΘ§Ζ÷±π «
Ϋχ––Ζ÷άύΧ÷¬έΘ§Ζ÷±π «![]() Θ§Φ¥Ω…«σ≥ωΫαΙϊΘ°
Θ§Φ¥Ω…«σ≥ωΫαΙϊΘ°
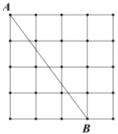
Θ®3Θ©ΗυΨίΧβ“βΩ…Ν–≥ω≤ΜΒ» Ϋ![]() Θ§”Οy±μ Ψ≥ωΝΫ≥«ΒΡΉήΖ―”ΟΘ§’β―υΨΆΩ…“‘ΗυΨίΚ· ΐΒΡ–‘÷ ≈–ΕœΘ°
Θ§”Οy±μ Ψ≥ωΝΫ≥«ΒΡΉήΖ―”ΟΘ§’β―υΨΆΩ…“‘ΗυΨίΚ· ΐΒΡ–‘÷ ≈–ΕœΘ°
(1)“ρΈΣ…η¥”A≥«‘ΥΆυCœγΒΡΖ ΝœΈΣxtΘ§‘ρ¥”A≥«‘ΥΆυDœγΖ®»ΥΖ ΝœΈΣ![]() Θ§¥”B≥«‘ΥΆυCœγΒΡΖ ΝœΈΣ
Θ§¥”B≥«‘ΥΆυCœγΒΡΖ ΝœΈΣ![]() Θ§
Θ§
Γύ¥”B≥«‘ΥΆυDœγΒΡΖ ΝœΈΣ![]()
Γύ![]() ,
,![]()
(2)”…![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
ΓύΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§![]() ≥«ΒΡΉή‘ΥΖ―Ϋœ…Ό
≥«ΒΡΉή‘ΥΖ―Ϋœ…Ό
Β±![]() ±Θ§
±Θ§![]() Θ§ΝΫ≥«ΒΡΉή‘ΥΖ―œύΒ»Θ§
Θ§ΝΫ≥«ΒΡΉή‘ΥΖ―œύΒ»Θ§
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§![]() ≥«ΒΡΉή‘ΥΖ―Ϋœ…Ό
≥«ΒΡΉή‘ΥΖ―Ϋœ…Ό
Θ®3Θ©”…![]() ΒΟ
ΒΟ![]() Θ§
Θ§
![]()
…ηΝΫ≥«Ήή‘ΥΖ―ΚΆΈΣ![]() Θ§‘ρ
Θ§‘ρ![]()
![]() Θ§
Θ§
Γύ![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχΦθ–ΓΘ§
ΒΡ‘ω¥σΕχΦθ–ΓΘ§
ΓύΒ±![]() ±Θ§
±Θ§![]() ”–Ήν–Γ÷Β
”–Ήν–Γ÷Β![]()

 ≈ύ”≈»ΐΚΟ…ζœΒΝ–¥πΑΗ
≈ύ”≈»ΐΚΟ…ζœΒΝ–¥πΑΗ ”≈Μ·Ής“Β…œΚΘΩΤΦΦΈΡœΉ≥ωΑφ…γœΒΝ–¥πΑΗ
”≈Μ·Ής“Β…œΚΘΩΤΦΦΈΡœΉ≥ωΑφ…γœΒΝ–¥πΑΗ