题目内容
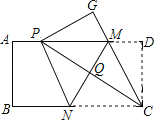
【题目】如图,先有一张矩形纸片![]() 点
点![]() 分别在矩形的边
分别在矩形的边![]() 上,将矩形纸片沿直线MN折叠,使点
上,将矩形纸片沿直线MN折叠,使点![]() 落在矩形的边
落在矩形的边![]() 上,记为点
上,记为点![]() ,点
,点![]() 落在
落在![]() 处,连接
处,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:
.下列结论:
![]()
②四边形![]() 是菱形;
是菱形;
③![]() 重合时,
重合时,![]() ;
;
④![]() 的面积
的面积![]() 的取值范围是
的取值范围是![]()
其中正确的是_____(把正确结论的序号都填上).
【答案】②③
【解析】
先判断出四边形![]() 是平行四边形,再根据翻折的性质可得
是平行四边形,再根据翻折的性质可得![]() ,然后根据邻边相等的平行四边形是菱形证明,判断出②正确;假设
,然后根据邻边相等的平行四边形是菱形证明,判断出②正确;假设![]() 得
得![]() ,进而得
,进而得![]() ,这个不一定成立,判断①错误;点
,这个不一定成立,判断①错误;点![]() 与点
与点![]() 重合时,设
重合时,设![]() ,表示出
,表示出![]() ,利用勾股定理列出方程求解得
,利用勾股定理列出方程求解得![]() 的值,进而用勾股定理求得
的值,进而用勾股定理求得![]() ,判断出③正确;当
,判断出③正确;当![]() 过
过![]() 点时,求得四边形
点时,求得四边形![]() 的最小面积,进而得
的最小面积,进而得![]() 的最小值,当
的最小值,当![]() 与
与![]() 重合时,
重合时,![]() 的值最大,求得最大值便可.
的值最大,求得最大值便可.
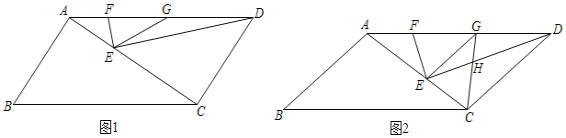
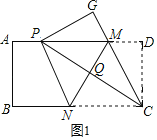
如图1,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() 四边形
四边形![]() 是菱形,故②正确;
是菱形,故②正确;
![]()
![]()
![]()
若![]() ,则
,则![]()
![]() ,这个不一定成立,
,这个不一定成立,
故①错误;
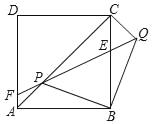
点![]() 与点
与点![]() 重合时,如图2,
重合时,如图2,
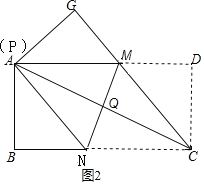
设![]() 则
则![]()
在![]()
即![]()
解得![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故③正确;
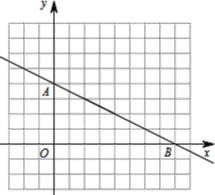
当![]() 过点
过点![]() 时,如图3,
时,如图3,
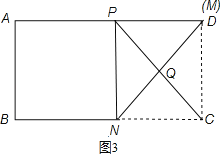
此时,![]() 最短,四边形
最短,四边形![]() 的面积最小,则
的面积最小,则![]() 最小为
最小为![]() ,
,
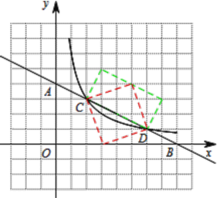
当![]() 点与
点与![]() 点重合时,
点重合时,![]() 最长,四边形
最长,四边形![]() 的面积最大,则
的面积最大,则![]() 最大为
最大为![]() ,
,
![]() ,
,
故④错误.
故答案为:②③.

练习册系列答案
相关题目