题目内容
2.如图1,△ABC内接于⊙O,AB为直径,∠CAE=∠B(1)试判断AE与⊙O的位置关系,并说明理由;
(2)若AB为非直径的弦,如图2,AE是⊙O的切线吗?为什么?
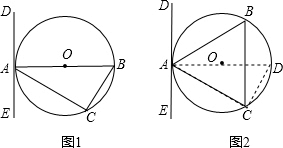
分析 (1)因为直线DE经过圆上A点,所以欲证AE是切线,只需证明DE⊥AB,即证∠EAB=90°即可.根据直径所对的圆周角是直角代换后可证;
(2)连接AO并延长交圆于点D,连接DC,构造(1)的图形,运用相同思路可证是切线.
解答  解:(1)AE是⊙O的切线
解:(1)AE是⊙O的切线
理由:如图1,
∵AB是直径,∴∠ACB=90°.
∴∠B+∠CAB=90°.
∵∠EAC=∠B,
∴∠EAC+∠CAB=90°,即∠EAB=90°,
∴AE是⊙O的切线;
(2)AE是切线.理由如下:
如图2,连接AO并延长交圆于点D,连接DC.
∵∠B=∠D,∠CAE=∠B,
∴∠CAE=∠D.
根据(1)的证明可知,AE是⊙O的切线
点评 本题考查了切线的判定、圆周角定理、三角形的内角和定理等知识点,注意:经过半径的外端且垂直于半径的直线是圆的切线,直径所对的圆周角是直角.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
10.在实数-2、0、2、-3中,最小的实数是( )
| A. | -2 | B. | 0 | C. | 2 | D. | -3 |
17.计算正确的是(a+3b)(a-3b)等于( )
| A. | a2-3b2 | B. | a2-9b2 | C. | a2+9b2 | D. | a2+3b2 |
7.下列计算正确的是( )
| A. | 2x2-3x2=-1 | B. | 2x•x=2x2 | C. | 6x6÷2x2=3x3 | D. | 2x+x=2x2 |
14.某商场第一季度的总利润是100万元,其中一月份的利润是20万元,设平均每月利润增长率为x,则依题意列出方程为( )
| A. | 20(1+x)2=100 | B. | 20+20x+20x2=100 | ||
| C. | 20+20(1+x)+20(1+x)2=100 | D. | 20(1+x)=100 |
11.2014年某市提出了总计约2450万元的投资计划,将2450万用科学记数法表示应为( )
| A. | 2.45×103 | B. | 2.45×106 | C. | 0.245×107 | D. | 2.45×107 |
12.与点P(-3,4)关于原点对称的点Q的坐标为( )
| A. | (-3,-4) | B. | (3,-4) | C. | (3,4) | D. | (4,-3) |




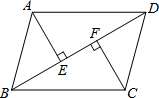 如图,平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,∠ABC=75°,∠DBC=30°,BC=2,则BD的长度为1+$\sqrt{3}$.
如图,平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,∠ABC=75°,∠DBC=30°,BC=2,则BD的长度为1+$\sqrt{3}$.