题目内容
1.某市举行中小学生器乐交流比赛,有45支队伍参赛,他们参赛的成绩各不相同,要取前23名获奖,某代表队已经知道了自己的成绩,他们想知道自己是否获奖,只需再知道这45支队伍成绩的( )| A. | 中位数 | B. | 平均数 | C. | 最高分 | D. | 方差 |
分析 由于有45支队伍参加全市中小学生器乐交流比赛,要取前23名获奖,故应考虑中位数的大小.
解答 解:共有45支队伍参加全市中小学生器乐交流比赛,要取前23名获奖,所以某代表队已经知道了自己的成绩是否进入前23名.我们把所有同学的成绩按大小顺序排列,第23名的成绩是这组数据的中位数,此代表队知道这组数据的中位数,才能知道自己是否获奖.
故选:A.
点评 本题考查了用中位数的意义解决实际问题.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.

练习册系列答案
相关题目
11.下列分式中,最简分式是( )
| A. | $\frac{4}{2x}$ | B. | $\frac{2x}{{x}^{2}+1}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{{x}^{2}}{xy}$ |
6.下列命题中,正确的是( )
| A. | 相等的角是对顶角 | |
| B. | 过一点有且只有一条直线与已知直线平行 | |
| C. | 两条不相交的线段一定互相平行 | |
| D. | 互为邻补角的两角的角平分线互相垂直 |
10.在实数-2、0、2、-3中,最小的实数是( )
| A. | -2 | B. | 0 | C. | 2 | D. | -3 |
11.2014年某市提出了总计约2450万元的投资计划,将2450万用科学记数法表示应为( )
| A. | 2.45×103 | B. | 2.45×106 | C. | 0.245×107 | D. | 2.45×107 |




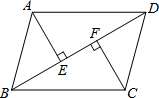 如图,平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,∠ABC=75°,∠DBC=30°,BC=2,则BD的长度为1+$\sqrt{3}$.
如图,平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,∠ABC=75°,∠DBC=30°,BC=2,则BD的长度为1+$\sqrt{3}$.