题目内容
1.已知△ABC,∠C=90°,AC=3,BC=6,CD是斜边AB上的高,且AD:AB=1:5,求AD,CD的长(要求画出图形)分析 首先根据题意画出符合题意的图形,由已知条件利用勾股定理易求AB的长,根据AB和AD的数量关系可求出AD的长,再利用勾股定理即可求出CD的长.
解答 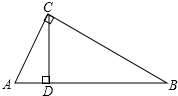 解:如图所示:
解:如图所示:
∵∠C=90°,AC=3,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=3$\sqrt{5}$,
∵AD:AB=1:5,
∴AD=$\frac{3\sqrt{5}}{5}$,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{\frac{180}{25}}$=$\frac{6\sqrt{5}}{5}$.
点评 本题考查了勾股定理的运用,解题的关键是熟记定理的内容即在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
12. 如图,DF∥AC,DE∥BC,下列各式中正确的有( )
如图,DF∥AC,DE∥BC,下列各式中正确的有( )
(1)$\frac{AD}{AB}$=$\frac{AE}{AC}$;(2)$\frac{AD}{AB}$=$\frac{CF}{BC}$;(3)$\frac{AD}{BD}$=$\frac{AE}{DF}$;(4)$\frac{AE}{CE}$=$\frac{CF}{BF}$.
 如图,DF∥AC,DE∥BC,下列各式中正确的有( )
如图,DF∥AC,DE∥BC,下列各式中正确的有( )(1)$\frac{AD}{AB}$=$\frac{AE}{AC}$;(2)$\frac{AD}{AB}$=$\frac{CF}{BC}$;(3)$\frac{AD}{BD}$=$\frac{AE}{DF}$;(4)$\frac{AE}{CE}$=$\frac{CF}{BF}$.
| A. | (1)(2) | B. | (1)(3) | C. | (1)(2)(3) | D. | (1)(2)(3)(4) |
16.下列说法错误的是( )
| A. | 若两数的差为0,则这两数必相等 | |
| B. | 较大的数减去较小的数,差一定是正数 | |
| C. | 两数之差一定小于被减数 | |
| D. | 减去一个负数,差一定大于被减数 |
 有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到与A相对的点B处,如图,已知杯子高8cm,点B距杯口3cm,杯子底面半径为4cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)
有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到与A相对的点B处,如图,已知杯子高8cm,点B距杯口3cm,杯子底面半径为4cm.蚂蚁从A点爬到B点的最短距离为多少?(π取3)