题目内容
定义运算“@”运算法则为：x@y＝
，则(2@6)@8＝__________
练习册系列答案
阅读快车系列答案
相关题目
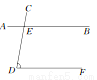
如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下面结论：①△ABD≌△EBC；②AC=2CD；③AD=AE=EC；④∠BCE+∠BCD=180°．其中正确的是（ ）
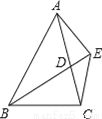
A. ①②③ B. ①②④ C. ①③④ D. ②③④
C 【解析】已知BD为△ABC的角平分线，根据角平分线的定义可得∠ABD=∠CBD，在△ABD和△EBC中，BD＝BC，∠ABD＝∠CBD，BE＝BA，由SAS可判定△ABD≌△EBC，即可得①正确；根据已知条件，无法证明AC=2CD，②错误； 已知BD为△ABC的角平分线，BD=BC，BE=BA，可得∠BCD=∠BDC=∠BAE=∠BEA， 再由∠BCE=∠BDA，∠BCE=∠BCD+∠D...已知：在△ABC中，∠A=60°，如要判定△ABC是等边三角形，还需添加一个条件．现有下面三种说法：
①如果添加条件“AB=AC”，那么△ABC是等边三角形；
②如果添加条件“∠B=∠C”，那么△ABC是等边三角形；
③如果添加条件“边AB、BC上的高相等”，那么△ABC是等边三角形．
上述说法中，正确的有（ ）
A. 3个 B. 2个 C. 1个 D. 0个
查看答案如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于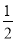
BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠A=50°，则∠ACB的度数为（ ）
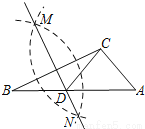
A. 90° B. 95° C. 100° D. 105°
查看答案如图，在△ABC中，AB=AC，D为BC上一点，且DA=DC，BD=BA，则∠B的大小为
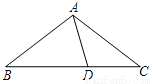
A. 40° B. 36° C. 30° D. 25°
查看答案如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )
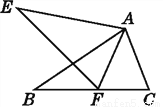
A. 1个 B. 2个 C. 3个 D. 4个
查看答案在平面直角坐标系中．点P（1，﹣2）关于x轴对称的点的坐标是（ ）
A. （1，2） B. （﹣1，﹣2） C. （﹣1，2） D. （﹣2，1）
查看答案 试题属性- 题型：单选题
- 难度：困难
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
， 
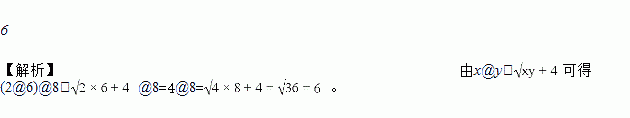
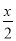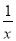，x－2，－10a2，0.8中，单项式有________________．
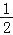线段MN为半径画弧，过两弧的交点的直线a就是所求作的垂线．