题目内容
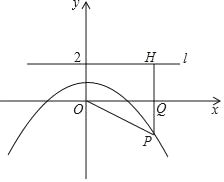
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线BC的解析式为y=﹣x+6.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线BC的解析式为y=﹣x+6.
(1)求抛物线的解析式;
(2)点M为线段BC上方抛物线上的任意一点,连接MB,MC,点N为抛物线对称轴上任意一点,当M到直线BC的距离最大时,求点M的坐标及MN+NB的最小值;
(3)在(2)中,点M到直线BC的距离最大时,连接OM交BC于点E,将原抛物线沿射线OM平移,平移后的抛物线记为y′,当y′经过点M时,它的对称轴与x轴的交点记为H.将△BOE绕点B逆时针旋转60°至△BO1E1,再将△BO1E1沿着直线O1H平移,得到△B1O2E2,在平面内是否存在点F,使以点C,H,B1,F为顶点的四边形是以B1H为边的菱形.若存在,直接写出点B1的横坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2+2x+6;(2)点M的坐标及MN+NB的最小值分别为:(3,
x2+2x+6;(2)点M的坐标及MN+NB的最小值分别为:(3,![]() ),
),![]() ;(3)存在,此时,点B1的横坐标为18.
;(3)存在,此时,点B1的横坐标为18.
【解析】
(1)直线BC的解析式为y=-x+6,则B(6,0)、C(0,6),把B、C坐标代入二次函数表达式,解得:y=-![]() x2+2x+6;
x2+2x+6;
(2)设M横坐标为t,则M到直线BC的距离为d=![]() =
=![]() ;点B关于对称轴的对称点为A,则AM为MN+NB的最小值,即可求解;
;点B关于对称轴的对称点为A,则AM为MN+NB的最小值,即可求解;
(3)OM所在直线方程为:y=![]() x,当抛物线沿OM直线平移时,设顶点向右平移2m,则向上平移了5m,新顶点坐标为(2+2m,8+5m),则y′=-
x,当抛物线沿OM直线平移时,设顶点向右平移2m,则向上平移了5m,新顶点坐标为(2+2m,8+5m),则y′=-![]() (x-2-2m)2+(8+5m),把点M(3,
(x-2-2m)2+(8+5m),把点M(3,![]() )代入上式,解得:m=
)代入上式,解得:m=![]() ,则H(9,0).①假设:平行四边形处于CF′HB′1位置时,该四边形为菱形,则B′1的y坐标为6,则其x坐标为9+2
,则H(9,0).①假设:平行四边形处于CF′HB′1位置时,该四边形为菱形,则B′1的y坐标为6,则其x坐标为9+2![]() ,而B′1C=9+2
,而B′1C=9+2![]() ,B′1H=4
,B′1H=4![]() ,即:B′1C≠B′1H,CF′HB′1不是菱形;②假设:平行四边形处于CHB1F位置时,该四边形为菱形,则B1的横坐标为2OH=18.
,即:B′1C≠B′1H,CF′HB′1不是菱形;②假设:平行四边形处于CHB1F位置时,该四边形为菱形,则B1的横坐标为2OH=18.
(1)直线BC的解析式为y=﹣x+6,则B(6,0)、C(0,6),
把点B、C坐标代入二次函数表达式,
解得:y=﹣![]() x2+2x+6,
x2+2x+6,
此时,顶点坐标为(2,8),A(﹣2,0);
(2)设M横坐标为t,则M到直线BC的距离为d=![]() =
=![]() ,
,
∴当t=3时,d最大,则M(3,![]() ),
),
点B关于对称轴的对称点为A,则AM为MN+NB的最小值,AM=![]() =
=![]() ;
;
∴点M的坐标及MN+NB的最小值分别为:(3,![]() ),
),![]() ;
;
(3)OM所在直线方程为:y=![]() x,
x,
当抛物线沿OM直线平移时,设顶点向右平移2m,则向上平移了5m,新顶点坐标为(2+2m,8+5m),
则y′=﹣![]() (x﹣2﹣2m)2+(8+5m),
(x﹣2﹣2m)2+(8+5m),
把点M(3,![]() )代入上式,解得:m=
)代入上式,解得:m=![]() ,(m=0舍去),则H(9,0),
,(m=0舍去),则H(9,0),
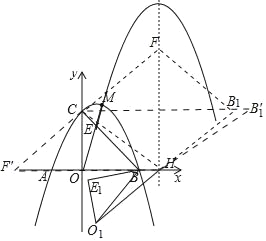
△BOE绕点B逆时针旋转60°至△BO1E1,此时,直线BO1的k值为![]() ,
,
再将△BO1E1沿着直线O1H平移,得到△B1O2E2,直线B1H的k也为![]() ,
,
则B1H所在的直线方程为:y=![]() x﹣9
x﹣9![]() ,
,
①假设:平行四边形处于CF′HB′1位置时,该四边形为菱形,则B′1的y坐标为6,则其x坐标为9+2![]() ,
,
而B′1C=9+2![]() ,B′1H=4
,B′1H=4![]() ,即:B′1C≠B′1H,CF′HB′1不是菱形;
,即:B′1C≠B′1H,CF′HB′1不是菱形;
②假设:平行四边形处于CHB1F位置时,该四边形为菱形,则B1的横坐标为2OH=18.
故:存在,此时,点B1的横坐标为18.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案