题目内容
8.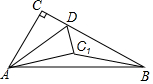 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C1处,连接C1B,则BC1的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C1处,连接C1B,则BC1的最小值为( )| A. | 2 | B. | 3 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 先根据含30度的直角三角形三边的关系得到AC=$\frac{1}{2}$AB=3,再利用折叠的性质得AC1=AC=3,然后利用三角形三边的关系得到BC1≥AB-AC1(当且仅当点C1在AB上时取等号),于是取等号可确定BC1的最小值.
解答 解:∵ACB=90°,∠ABC=30°,
∴AC=$\frac{1}{2}$AB=3,
∵△ACD沿AD折叠,点C落在点C1处,
∴AC1=AC=3,
∴BC1≥AB-AC1(当且仅当点C1在AB上时取等号),
∴点C1在AB上时,BC1的值最小,最小值为6-3=3.
故选B.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了含30度的直角三角形三边的关系和三角形三边的关系.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
18.已知实数a、b,若a>b,则下列结论正确的是( )
| A. | a-5=b-5 | B. | -2a>-2b | C. | $\frac{a}{3}$>$\frac{b}{3}$ | D. | 2a>3b |
3.2016年11月3日,中国首枚大型运载火箭长征五号在文昌航天发射场成功发射,它是我国新一代运载火箭,近地轨道运载能力约25吨级,起飞推力约为10500千牛,10500千牛用科学记数法可表示为( )
| A. | 105×105 | B. | 1.05×107 | C. | 1.05×108 | D. | 0.105×108 |
20. 如图,已知∠ACB是⊙O的圆周角,∠ACB=35°,则圆心角∠AOB是( )
如图,已知∠ACB是⊙O的圆周角,∠ACB=35°,则圆心角∠AOB是( )
 如图,已知∠ACB是⊙O的圆周角,∠ACB=35°,则圆心角∠AOB是( )
如图,已知∠ACB是⊙O的圆周角,∠ACB=35°,则圆心角∠AOB是( )| A. | 17.5° | B. | 35° | C. | 50° | D. | 70° |
18.下列式子合并同类项正确的是( )
| A. | 3x+5y=8xy | B. | 15ab-15ba=0 | C. | 3y2-y2=3 | D. | 7x3-6x2=x |