题目内容
16．把方程组$\left\{\begin{array}{l}{2x+3y=5}\\{3y-4z=3}\\{4z+5x=7}\end{array}\right.$消去未知数z，转化为只含x、y的方程组为$\left\{\begin{array}{l}{2x+3y=5}\\{5x+3y=12}\end{array}\right.$．分析 先把第2和和第3个方程相加消去z，然后把它与第1个方程可组成关于x、y的二元一次方程组．
解答 解：$\left\{\begin{array}{l}{2x+3y=5①}\\{3y-4z=3②}\\{4z+5x=7③}\end{array}\right.$，
②+③得5x+3y=10④，
由①④组成关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+3y=5}\\{5x+3y=12}\end{array}\right.$．
故答案为$\left\{\begin{array}{l}{2x+3y=5}\\{5x+3y=12}\end{array}\right.$．
点评 本题考查了解三元一次方程组：利用加减或代入消元法把解三元一次方程组的问题转化为解二元一次方程组的问题．
练习册系列答案
相关题目
7．
为有效保护日益减少的水资源，某市提倡居民节约用水，并对该市居民用水采取分段收费：每户每月用水不超过20m3，每立方米收费3元；若用水超过20m3，超过部分每立方米收费5元．该市某居民家8月份交水费84元，则该居民家8月份用水量为多少m3？如果设该居民家8月份用水量为xm3，则下面所列方程中正确的是（ ）
为有效保护日益减少的水资源，某市提倡居民节约用水，并对该市居民用水采取分段收费：每户每月用水不超过20m3，每立方米收费3元；若用水超过20m3，超过部分每立方米收费5元．该市某居民家8月份交水费84元，则该居民家8月份用水量为多少m3？如果设该居民家8月份用水量为xm3，则下面所列方程中正确的是（ ）| A． | 3x+5=84 | B． | 3×20+5x=84 | C． | 3×20+5（x-20）=84 | D． | 3x+5（x-20）=84 |
11．不等式-2x＜6变形为x＞-3的依据是（ ）
| A． | 不等式的性质1 | B． | 不等式的性质2 | C． | 不等式的性质3 | D． | 等式的基本性质2 |
1．越越是一位密码编译爱好者，在他的密码手册中，有这样一条信息，a-b，x-y，x+y，a+b，x2-y2，a2-b2分别对应下列六个字：城、爱、我、蒙、游、美，现将（x2-y2）a2-（x2-y2）b2因式分解，结果呈现的密码信息可能（ ）
| A． | 我爱美 | B． | 蒙城游 | C． | 爱我蒙城 | D． | 美我蒙城 |
8．
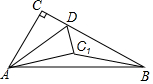如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，AB=6，点D是BC上一动点，连接AD，将△ACD沿AD折叠，点C落在点C1处，连接C1B，则BC1的最小值为（ ）
如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，AB=6，点D是BC上一动点，连接AD，将△ACD沿AD折叠，点C落在点C1处，连接C1B，则BC1的最小值为（ ）| A． | 2 | B． | 3 | C． | 3$\sqrt{2}$ | D． | 2$\sqrt{3}$ |
AB是⊙O的直径，AC是弦，OD∥AC，则∠ODB=90°．