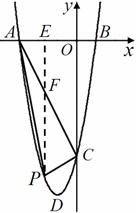
题目内容
已知某二次函数的图象与 轴分别相交于点
轴分别相交于点 和点
和点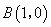 ,
,
与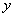 轴相交于点
轴相交于点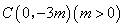 ,顶点为点
,顶点为点 。
。
⑴求该二次函数的解析式(系数用含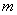 的代数式表示);
的代数式表示);
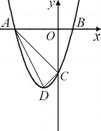
⑵如图①,当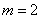 时,点
时,点 为第三象限内抛物线上的一个动点,设
为第三象限内抛物线上的一个动点,设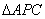 的面积为
的面积为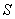 ,试求出
,试求出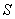 与点
与点 的横坐标
的横坐标 之间的函数关系式及
之间的函数关系式及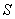 的最大值;
的最大值;
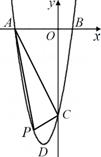
⑶如图②,当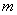 取何值时,以
取何值时,以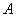 、
、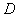 、
、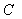 三点为顶点的三角形与
三点为顶点的三角形与 相似?
相似?
 | |||||
| |||||
| |||||
 解:⑴∵该二次函数的图象与
解:⑴∵该二次函数的图象与 轴分别相交于点
轴分别相交于点 和点
和点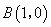 ,
,
∴设该二次函数的解析式为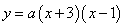
∵该二次函数的图象与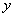 轴相交于点
轴相交于点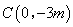 ,
,
∴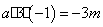 ,故
,故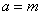
∴该二次函数的解析式为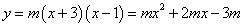
⑵当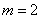 时,点
时,点 的坐标为
的坐标为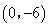 ,该二次函数的解析式为
,该二次函数的解析式为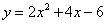
∵点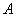 的坐标为
的坐标为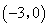 ,点
,点 的坐标为
的坐标为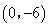
∴直线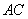 的解析式为
的解析式为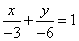 ,即
,即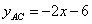
过点 作
作 轴于点
轴于点 ,交
,交 于点
于点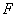
∵点 为第三象限内抛物线上的一个动点且点
为第三象限内抛物线上的一个动点且点 的横坐标为
的横坐标为
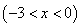
∴点 的坐标为
的坐标为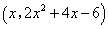 ,点
,点 的坐标为
的坐标为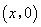 ,点
,点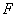 的坐标为
的坐标为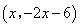
∴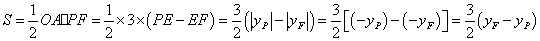
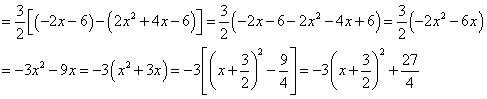
∴当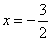 时,
时,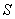 有最大值
有最大值 ;
;
另解: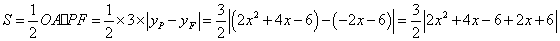
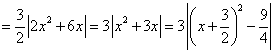
∵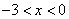 ,∴
,∴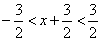 ,∴
,∴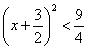 ,∴
,∴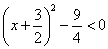 ,
,
∴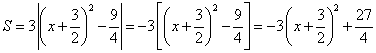 (其余略)
(其余略)
再解: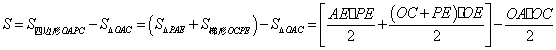
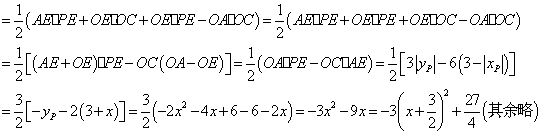
⑶∵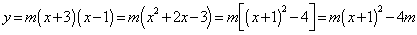 ,∴点
,∴点 的坐标为
的坐标为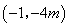
∴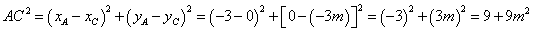
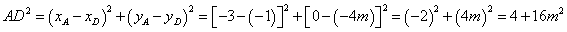
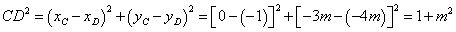
∵ 是直角三角形,∴欲使以
是直角三角形,∴欲使以 、
、 、
、 三点为顶点的三角形与
三点为顶点的三角形与 相似,必有
相似,必有
①若在 中,
中,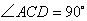 ,则
,则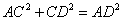 ,即
,即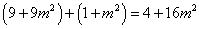
化简整理得: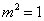 ,∵
,∵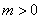 ,∴
,∴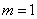 (舍去负值)
(舍去负值)
此时,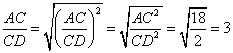 ,
,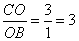 ,∴
,∴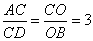
∵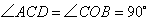 且
且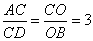 ,∴
,∴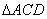 与
与 相似,符合题意;
相似,符合题意;
②若在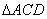 中,
中,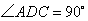 ,则
,则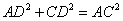 ,即
,即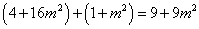
化简整理得: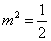 ,∵
,∵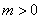 ,∴
,∴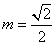 (舍去负值)
(舍去负值)
此时,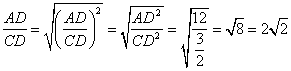 ,
,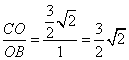 ,∴
,∴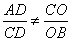
虽然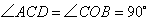 ,但是
,但是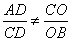 ,∴
,∴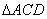 与
与 不相似,应舍去;
不相似,应舍去;
∴综上所述,只有当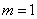 时,以
时,以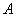 、
、 、
、 三点为顶点的三角形与
三点为顶点的三角形与 相似。
相似。

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 在实数范围内有意义,则
在实数范围内有意义,则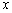 的取值范围是________________.
的取值范围是________________. 上任意一点, l是过点(0,
上任意一点, l是过点(0, )且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.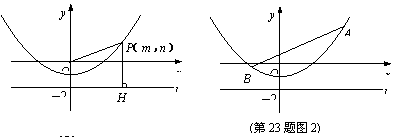
 ,
, ,
, ,
, ,则成绩较稳定的是。(填“甲”或“乙”)
,则成绩较稳定的是。(填“甲”或“乙”) 中,
中, ,
, ,
, 于点
于点 于点
于点 ≌
≌ 。
。

 = .
= .