题目内容
 已知,如图,A是圆O外一点,AO的延长线交圆O于点C,点B在圆上,且AB=BC,∠A=30°,求证:AB是圆O的切线.
已知,如图,A是圆O外一点,AO的延长线交圆O于点C,点B在圆上,且AB=BC,∠A=30°,求证:AB是圆O的切线.考点:切线的判定
专题:证明题
分析:连接OB,由AB=BD,利用等边对等角得到∠A=∠D=30°,再由OB=OD,利用等边对等角得到∠OBD=30°,利用外角的性质得到∠AOB=60°,再2三角形AOB中,利用内角和定理得到∠ABO为直角,即AB垂直与OB,即可得证.
解答: 证明:连接OB,
证明:连接OB,
∵AB=DB,
∴∠A=∠D=30°,
∵OD=OB,
∴∠D=∠OBD=30°,
∵∠AOB为△BOD的外角,
∴∠AOB=2∠D=60°,
在△OAB中,∠A=30°,∠AOB=60°,
∴∠ABO=90°,即AB⊥OB,
则AB是圆O的切线.
 证明:连接OB,
证明:连接OB,∵AB=DB,
∴∠A=∠D=30°,
∵OD=OB,
∴∠D=∠OBD=30°,
∵∠AOB为△BOD的外角,
∴∠AOB=2∠D=60°,
在△OAB中,∠A=30°,∠AOB=60°,
∴∠ABO=90°,即AB⊥OB,
则AB是圆O的切线.
点评:此题考查了切线的判定方法,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
相关题目
 在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).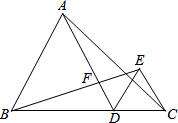 已知:如图,点D是线段BC上的任意一点,△ABD和△DCE都是等边三角形,AD与BE交于点F.
已知:如图,点D是线段BC上的任意一点,△ABD和△DCE都是等边三角形,AD与BE交于点F. 如图,边长为1的小正方形网格中,⊙O的圆心O及A、B、C、E均在格点上,BC交⊙O于D,则∠AED的余弦值是
如图,边长为1的小正方形网格中,⊙O的圆心O及A、B、C、E均在格点上,BC交⊙O于D,则∠AED的余弦值是