题目内容
18．方程ax2+bx+c=0的两根为-3，1，则抛物线y=ax2+bx+c的对称轴是直线x=-1．分析 由条件可求得抛物线与x轴的两个交点的横坐标，再利用对称性可求得抛物线线的对称轴．
解答 解：
∵方程ax2+bx+c=0的两根为-3，1，
∴抛物线y=ax2+bx+c与x轴的两个交点坐标为（-3，0）和（1，0），
∴抛物线对称轴x=$\frac{-3+1}{2}$=-1，
故答案为：x=-1．
点评 本题主要考查二次函数的性质，掌握二次函数的图象与x轴的交点的横坐标即为相应一元二次方程的根是解题的关键．
练习册系列答案
相关题目
如图，一架梯子长25米，斜靠在一面墙上，梯子顶端离地面15米，要使梯子顶端离地24米，则梯子的底部在水平方向上应滑动多少米？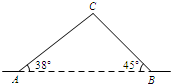
如图，从A地到B地的公路需经过C地，AC=10千米，∠CAB=38°，∠ABC=45°．因城市规划的需要，将在A、B两地之间修建一条笔直的公路．求改直后的公路AB的长（精确到1千米）．（参考数据：sin38°=0.62，cos38°=0.79，tan38°=0.78）
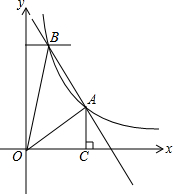如图，在平面直角坐标系xOy中，一次函数y1=kx+b（k≠0）的图象与反比例函数y2=$\frac{m}{x}$（m≠0，x＞0）的图象交于第一象限内的A、B两点，过点A作AC⊥x轴于点C，AC=3，点B的坐标为（2，6）
7．
如图所示的圆锥，它的主视图和俯视图分别是（ ）
如图所示的圆锥，它的主视图和俯视图分别是（ ）| A． | 等边三角形、圆 | B． | 等边三角形、等腰三角形 | ||
| C． | 等腰三角形、圆 | D． | 圆、等腰三角形 |