题目内容
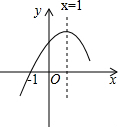 二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc>0;②2a-b;③9a+3b+c=0;④当x<-1或x>3时,y<0.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc>0;②2a-b;③9a+3b+c=0;④当x<-1或x>3时,y<0.其中正确的是( )| A、①②③ | B、②③④ |
| C、①③④ | D、③④ |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:根据图象可得:a<0,b>0,c>0.
则abc<0,故①错误;
抛物线的对称轴直线是x=1,即-
=1,则b+2a=0,故②错误;
当x=3时图象与x轴交于一点,所以9a+3b+c=0,故③正确;
根据图示知,当x<-1或x>3时,y<0.故④正确.
综上所知,正确的是③④.
故选:D.
则abc<0,故①错误;
抛物线的对称轴直线是x=1,即-
| b |
| 2a |
当x=3时图象与x轴交于一点,所以9a+3b+c=0,故③正确;
根据图示知,当x<-1或x>3时,y<0.故④正确.
综上所知,正确的是③④.
故选:D.
点评:此题考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
相关题目
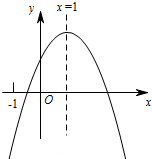 观察二次函数y=ax2+bx+c(a≠0)的图象,下列四个结论:
观察二次函数y=ax2+bx+c(a≠0)的图象,下列四个结论:①4ac-b2>0;②4a+c<2b;③b+c<0;④n(an+b)-b<a(n≠1).
正确结论的个数是( )
| A、4个 | B、3个 | C、2个 | D、1个 |
 如图,扇形AOB是直角扇形,以OA、OB为直径在扇形内作半圆,M、N分别表示两个阴影部分的面积,那么M、N的大小关系是( )
如图,扇形AOB是直角扇形,以OA、OB为直径在扇形内作半圆,M、N分别表示两个阴影部分的面积,那么M、N的大小关系是( )| A、M>N | B、M=N |
| C、M<N | D、无法确定 |
 如图,将长方形纸片的角A、E分别沿着BC、BD折叠,则∠CBD的度数是( )
如图,将长方形纸片的角A、E分别沿着BC、BD折叠,则∠CBD的度数是( )| A、85° | B、90° |
| C、95° | D、100° |
如果
=
,那么
的值是( )
| x+y |
| y |
| 7 |
| 4 |
| y |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,矩形ABCD中,点F是BC上一点,AD=DF,AE⊥DF,垂足为E.求证:AE=AB.
如图,矩形ABCD中,点F是BC上一点,AD=DF,AE⊥DF,垂足为E.求证:AE=AB.