题目内容
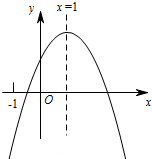 观察二次函数y=ax2+bx+c(a≠0)的图象,下列四个结论:
观察二次函数y=ax2+bx+c(a≠0)的图象,下列四个结论:①4ac-b2>0;②4a+c<2b;③b+c<0;④n(an+b)-b<a(n≠1).
正确结论的个数是( )
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:二次函数图象与系数的关系
专题:
分析:首先根据开口方向确定a的取值范围,根据对称轴的位置确定b的取值范围,根据抛物线与y轴的交点确定c的取值范围,根据抛物线与x轴是否有交点确定b2-4ac的取值范围,根据图象和x=-2的函数值即可确定4a-2b+c的取值范围,根据b、c的取值范围可以确定b+c<0是否成立.根据二次函数的最值问题得到an2+bn+c<a+b+c(n≠-1),即n(an+b)-b<a,则可对④进行判断.
解答:解:∵抛物线与x轴有两个交点,
∴b2-4ac>0,4ac-b2<0,故①错误.
根据图象知道当x=-2时,y=4a-2b+c<0,4a+c<2b,故②正确;
∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=-
,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,b+c>0,故③错误;
∵x=1时,函数值有最大值a+b+c,
∴an2+bn+c<a+b+c(n≠-1),
∴n(an+b)-b<a,所以④正确.
故选:C.
∴b2-4ac>0,4ac-b2<0,故①错误.
根据图象知道当x=-2时,y=4a-2b+c<0,4a+c<2b,故②正确;
∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=-
| b |
| 2a |
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,b+c>0,故③错误;
∵x=1时,函数值有最大值a+b+c,
∴an2+bn+c<a+b+c(n≠-1),
∴n(an+b)-b<a,所以④正确.
故选:C.
点评:本题考查了二次函数的图象与系数的关系,根据函数图象解答问题,体现了数形结合的数学思想方法.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
一组数据x1,x2,…,xn的方差为
,则数据5x1-2,5x2-2,…,5xn-2的方差为( )
| 1 |
| 5 |
| A、2 | B、1 | C、5 | D、8 |
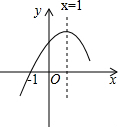 二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc>0;②2a-b;③9a+3b+c=0;④当x<-1或x>3时,y<0.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc>0;②2a-b;③9a+3b+c=0;④当x<-1或x>3时,y<0.其中正确的是( )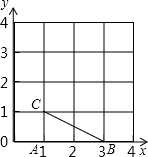 如图,在直角坐标系中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点).
如图,在直角坐标系中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点).