题目内容
 如图,将长方形纸片的角A、E分别沿着BC、BD折叠,则∠CBD的度数是( )
如图,将长方形纸片的角A、E分别沿着BC、BD折叠,则∠CBD的度数是( )| A、85° | B、90° |
| C、95° | D、100° |
考点:角的计算,翻折变换(折叠问题)
专题:
分析:利用角的相等关系和平角关系求出∠CBD的度数.
解答:解:根据题意得:∠A′BC=∠ABC,∠E′BD=∠EBD,
∵∠A′BC+∠ABC+∠E′BD+∠EBD=180°,
∴∠A′BC+∠E′BD=
×180°=90°,
即∠CBD=90°;
故选B.
∵∠A′BC+∠ABC+∠E′BD+∠EBD=180°,
∴∠A′BC+∠E′BD=
| 1 |
| 2 |
即∠CBD=90°;
故选B.
点评:此题主要考查了翻折变换以及平角的定义,解决问题的关键是根据翻折的方法得到两组相等的角,再根据它们的和是平角,即可得出结论.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
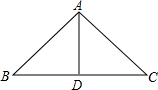 如图,在△ABC中,AB=AC,∠BAC=90°,AD⊥BC,则下列结论不正确的是( )
如图,在△ABC中,AB=AC,∠BAC=90°,AD⊥BC,则下列结论不正确的是( )| A、∠BAD=45° | ||
| B、△ABD≌△ACD | ||
C、AD=
| ||
D、AD=
|
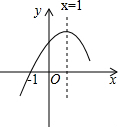 二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc>0;②2a-b;③9a+3b+c=0;④当x<-1或x>3时,y<0.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc>0;②2a-b;③9a+3b+c=0;④当x<-1或x>3时,y<0.其中正确的是( )| A、①②③ | B、②③④ |
| C、①③④ | D、③④ |
下列说法正确的是( )
| A、线段AB和线段BA是同一条线段 |
| B、射线AB和射线BA是同一条射线 |
| C、直线AB和直线BA是同一条线段 |
| D、射线AB和线段AB对应同一图形 |
函数y=a(x-1)2,y=ax+a的图象在同一坐标系的图象可能是( )
A、 |
B、 |
C、 |
D、 |