题目内容
如图，扇形AOB是直角扇形，以OA、OB为直径在扇形内作半圆，M、N分别表示两个阴影部分的面积，那么M、N的大小关系是（ ）| A、M＞N | B、M=N |
| C、M＜N | D、无法确定 |
考点：扇形面积的计算
专题：
分析：假设出扇形半径，再表示出半圆面积，以及扇形面积，进而即可表示出两部分阴影面积．
解答：解：∵扇形OAB的圆心角为90°，假设扇形半径为a，
∴扇形OAB面积为：
=
，
半圆面积为：
×π×（
）2=
，
∵M=
-2×
+N，
∴M=N．
故选：B．
∴扇形OAB面积为：
| 90πa2 |
| 360 |
| πa2 |
| 4 |
半圆面积为：
| 1 |
| 2 |
| a |
| 2 |
| πa2 |
| 8 |
∵M=
| πa2 |
| 4 |
| πa2 |
| 8 |
∴M=N．
故选：B．
点评：此题主要考查了扇形面积求法，根据已知得出半圆面积以及扇形面积是解题关键．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
某件商品，打八折销售后是a元，则原价是（ ）元．
| A、0.8a | ||
B、
| ||
C、
| ||
| D、1.8a |
一组数据x1，x2，…，xn的方差为
，则数据5x1-2，5x2-2，…，5xn-2的方差为（ ）
| 1 |
| 5 |
| A、2 | B、1 | C、5 | D、8 |
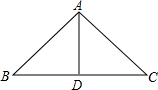如图，在△ABC中，AB=AC，∠BAC=90°，AD⊥BC，则下列结论不正确的是（ ）| A、∠BAD=45° | ||
| B、△ABD≌△ACD | ||
C、AD=
| ||
D、AD=
|
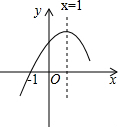二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，0），图象的对称轴是直线x=1，其图象的一部分如图所示，对于下列说法：①abc＞0；②2a-b；③9a+3b+c=0；④当x＜-1或x＞3时，y＜0．其中正确的是（ ）| A、①②③ | B、②③④ |
| C、①③④ | D、③④ |
下列说法正确的是（ ）
| A、线段AB和线段BA是同一条线段 |
| B、射线AB和射线BA是同一条射线 |
| C、直线AB和直线BA是同一条线段 |
| D、射线AB和线段AB对应同一图形 |