题目内容
 如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是
如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是考点:三角形中位线定理,全等三角形的判定与性质
专题:
分析:连接DE并延长交AB于H,证明△DCE≌△HAE,根据全等三角形的性质可得DE=HE,DC=AH,则EF是△DHB的中位线,再根据中位线的性质可得答案.
解答: 解:连接DE并延长交AB于H.
解:连接DE并延长交AB于H.
∵CD∥AB,
∴∠C=∠A,
∵E是AC中点,
∴DE=EH,
在△DCE和△HAE中,
,
∴△DCE≌△HAE(ASA),
∴DE=HE,DC=AH,
∵F是BD中点,
∴EF是△DHB的中位线,
∴EF=
BH,
∴BH=AB-AH=AB-DC=2,
∴EF=1.
 解:连接DE并延长交AB于H.
解:连接DE并延长交AB于H.∵CD∥AB,
∴∠C=∠A,
∵E是AC中点,
∴DE=EH,
在△DCE和△HAE中,
|
∴△DCE≌△HAE(ASA),
∴DE=HE,DC=AH,
∵F是BD中点,
∴EF是△DHB的中位线,
∴EF=
| 1 |
| 2 |
∴BH=AB-AH=AB-DC=2,
∴EF=1.
点评:此题主要考查了全等三角形的判定与性质,以及三角形中位线性质,关键是正确画出辅助线,证明△DCE≌△HAE.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
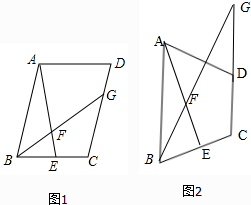 如图1,在?ABCD中,点E是BC边的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若
如图1,在?ABCD中,点E是BC边的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若 如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则平行四边形ABCD的周长为
如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则平行四边形ABCD的周长为