题目内容
 如图,点A,B,C是小正方形的顶点,求∠ABC的度数.
如图,点A,B,C是小正方形的顶点,求∠ABC的度数.考点:勾股定理的逆定理,勾股定理,等腰直角三角形
专题:网格型
分析:连接AC.分别在格点三角形中,根据勾股定理得到AB,BC,AC的长度,从而得出△ABC是等腰直角三角形,继而可得出∠ABC的度数.
解答: 解:连接AC.
解:连接AC.
根据勾股定理可以得到:AC=BC=
,AB=
,
∵(
)2+(
)2=(
)2,即AC2+BC2=AB2,
∴△ABC是等腰直角三角形,
∴∠ABC=45°.
 解:连接AC.
解:连接AC.根据勾股定理可以得到:AC=BC=
| 10 |
| 20 |
∵(
| 10 |
| 10 |
| 20 |
∴△ABC是等腰直角三角形,
∴∠ABC=45°.
点评:本题考查了勾股定理及其逆定理,判断△ABC是等腰直角三角形是解决本题的关键,注意在格点三角形中利用勾股定理.

练习册系列答案
相关题目
下列选项中,与x2y是同类项的是( )
| A、.-2x2y |
| B、-2xy2 |
| C、xy |
| D、x2y2 |
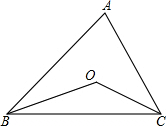 如图,点O是△ABC两内角平分线的交点
如图,点O是△ABC两内角平分线的交点 如图,在数轴上有若干个点每相邻两点之间的距离是1个单位长,有理数a,b,c,d 所表示的点是其中的4个,且在数轴上的位置如图所示.设3a=4b-3,求c+2d的值.
如图,在数轴上有若干个点每相邻两点之间的距离是1个单位长,有理数a,b,c,d 所表示的点是其中的4个,且在数轴上的位置如图所示.设3a=4b-3,求c+2d的值.