题目内容
7.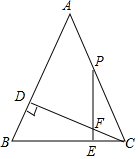 已知:在△ABC中,AB=AC,CD是AB边上的高,点P是AC边上任意一点(不与点A、点C重合)过点P作PE⊥BC,垂足为E,交CD于点F.若AD=CD,探究线段PF、CE之间的数量关系,并证明你的结论.
已知:在△ABC中,AB=AC,CD是AB边上的高,点P是AC边上任意一点(不与点A、点C重合)过点P作PE⊥BC,垂足为E,交CD于点F.若AD=CD,探究线段PF、CE之间的数量关系,并证明你的结论.
分析 根据AA可证△PCE∽△CBD∽△CFE,根据相似三角形的性质可得$\frac{PE-EF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,进一步得到$\frac{PF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,设CD=x,则AD=x,AB=AC=$\sqrt{2}$x,BD=AB-AD=($\sqrt{2}$-1)a,再代入计算即可求解.
解答 解:∵CD是AB边上的高,PE⊥BC,
∴∠BDC=∠PEC=90°,
∴∠DCB=90°-∠B,∠CPE=90°-∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠DCB=∠CPE,
∴△PCE∽△CBD∽△CFE,
∴$\frac{PE}{CD}$=$\frac{CE}{BD}$,$\frac{EF}{BD}$=$\frac{CE}{CD}$,
即$\frac{PE}{CE}$=$\frac{CD}{BD}$①,$\frac{EF}{CE}$=$\frac{BD}{CD}$②,
①-②$\frac{PE-EF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,
∵PE-EF=PF,
∴$\frac{PF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,
设CD=x,则AD=x,AB=AC=$\sqrt{2}$x,
∴BD=AB-AD=($\sqrt{2}$-1)a,
∴$\frac{PF}{CE}$=$\frac{a}{(\sqrt{2}-2)a}$-$\frac{(\sqrt{2}-1)a}{a}$=2,
∴PF=2CE.
点评 此题考查了等腰三角形的性质,相似三角形的判定和性质,关键是证明△PCE∽△CBD∽△CFE.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
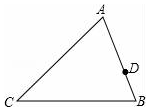 如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=$\frac{2}{3}$AB,在AC上取一点E,使以A、D、E为顶点的三角形与ABC相似,则AE等于10或6.4.
如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=$\frac{2}{3}$AB,在AC上取一点E,使以A、D、E为顶点的三角形与ABC相似,则AE等于10或6.4.