题目内容
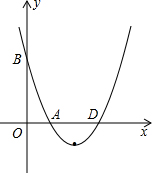 已知抛物线y=ax2+bx+c的图象经过点A(1,0),B(0,3),C(2,-1).
已知抛物线y=ax2+bx+c的图象经过点A(1,0),B(0,3),C(2,-1).(1)求该抛物线的解析式;
(2)求该抛物线与x轴的另一个交点D的坐标;
(3)该抛物线的对称轴上是否存在一点P,使得PA+PB最短?若点P存在,求出点P的坐标;若P点不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)将已知点的坐标代入二次函数的一般形式利用待定系数法确定抛物线的解析式即可;
(2)令y=0得到有关x的一元二次方程即可求得另一交点D的坐标;
(3)首先根据抛物线的解析式确定抛物线的对称轴,然后得到A关于对称轴x=2的对称点为点D,连接BD,则直线BD与对称轴x=2的交点即为点P,利用待定系数法确定直线BD的解析式后即可确定点P的坐标.
(2)令y=0得到有关x的一元二次方程即可求得另一交点D的坐标;
(3)首先根据抛物线的解析式确定抛物线的对称轴,然后得到A关于对称轴x=2的对称点为点D,连接BD,则直线BD与对称轴x=2的交点即为点P,利用待定系数法确定直线BD的解析式后即可确定点P的坐标.
解答:解:(1)把A(1,0),B(0,3),C(2,-1)代入y=ax2+bx+c,
得
,
解得
,
所以抛物线的解析式为y=x2-4x+3.
(2)令x2-4x+3=0,解得x1=1,x2=3.
∵点A的坐标为(1,0),
∴点D的坐标为(3,0).
(3)存在.
由(1)知该抛物线的对称轴为x=-
=-
=2,
点A关于对称轴x=2的对称点为点D,连接BD,则直线BD与对称轴x=2的交点即为点P.
令直线BD的解析式为y=kx+b,代入点B(0,3)和点D(3,0),
得
,
解得
所以直线BD的解析式为y=-x+3.
当x=2时,y=-2+3=1,
所以点P(2,1).
得
|
解得
|
所以抛物线的解析式为y=x2-4x+3.
(2)令x2-4x+3=0,解得x1=1,x2=3.
∵点A的坐标为(1,0),
∴点D的坐标为(3,0).
(3)存在.
由(1)知该抛物线的对称轴为x=-
| b |
| 2a |
| -4 |
| 2×1 |
点A关于对称轴x=2的对称点为点D,连接BD,则直线BD与对称轴x=2的交点即为点P.
令直线BD的解析式为y=kx+b,代入点B(0,3)和点D(3,0),
得
|
解得
|
所以直线BD的解析式为y=-x+3.
当x=2时,y=-2+3=1,
所以点P(2,1).
点评:本题考查了二次函数的综合知识,题目中设计到了最短线路问题、待定系数法确定一次函数和二次函数的解析式问题,综合性较强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个正方形的面积是15,估计它的边长大小在( )
| A、5与6之间 |
| B、4与5之间 |
| C、3与4之间 |
| D、2与3之间 |
已知xa=3,xb=4,则x3a-2b=( )
A、
| ||
B、
| ||
| C、11 | ||
| D、19 |
若
=
,则下列不正确是( )
| x |
| 2 |
| y |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各题中的两个项,不属于同类项的是( )
A、2x2y与-
| ||
| B、1与-32 | ||
| C、a2b与3×102ba2 | ||
D、
|

 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以这两个交点和该抛物线的顶点、对称轴上一点为顶点的菱形称为这条抛物线的“抛物菱形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以这两个交点和该抛物线的顶点、对称轴上一点为顶点的菱形称为这条抛物线的“抛物菱形”.