题目内容
根据学过的数学知识我们知道:任何数的平方都是一个非负数,即:对于任何数a,a2≥0都成立,据些请回答下列问题:
应用:代数式m2-1有 值(填“最大”或“最小”),
这个值是 ,此时m= ;
探究:求代数式n2+4n+5的最小值,小明是这样做的:
n2+4n+5=n2+4n+4+1
=(n+2)2+1
∴当n=-2时,代数式有最小值,最小值为1
请你按照小明的方法,求代数式4x2+12x-1的最小值,并求此时x的值.
拓展:求多项式x2-4xy+5y2-12y+15的最小值及此时x、y的值.
应用:代数式m2-1有
这个值是
探究:求代数式n2+4n+5的最小值,小明是这样做的:
n2+4n+5=n2+4n+4+1
=(n+2)2+1
∴当n=-2时,代数式有最小值,最小值为1
请你按照小明的方法,求代数式4x2+12x-1的最小值,并求此时x的值.
拓展:求多项式x2-4xy+5y2-12y+15的最小值及此时x、y的值.
考点:配方法的应用,非负数的性质:偶次方
专题:阅读型
分析:根据非负数的性质即可得出答案;先把给出的式子化成完全平方的形式,再根据非负数的性质即可得出答案.
解答:解:代数式m2-1有最小值,
这个值是-1,此时m=0;
∵4x2+12x-1=(2x+3)2-10,
∴当2x+3=0,即x=-
时,代数式4x2+12x-1的最小值为-10;
∵x2-4xy+5y2-12y+15
=x2-4xy+4y2+y2-12y+15
=(x-2y)2+(y-6)2-21,
∴当x-2y=0,y-6=0时,即x=12,y=6多项式x2-4xy+5y2-12y+15的最小值是-21.
这个值是-1,此时m=0;
∵4x2+12x-1=(2x+3)2-10,
∴当2x+3=0,即x=-
| 3 |
| 2 |
∵x2-4xy+5y2-12y+15
=x2-4xy+4y2+y2-12y+15
=(x-2y)2+(y-6)2-21,
∴当x-2y=0,y-6=0时,即x=12,y=6多项式x2-4xy+5y2-12y+15的最小值是-21.
点评:此题考查了因式分解的应用,用到的知识点是完全平方公式,非负数的性质,解题的关键是把给出的式子化成完全平方的性质进行解答.

练习册系列答案
相关题目
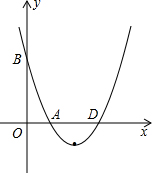 已知抛物线y=ax2+bx+c的图象经过点A(1,0),B(0,3),C(2,-1).
已知抛物线y=ax2+bx+c的图象经过点A(1,0),B(0,3),C(2,-1).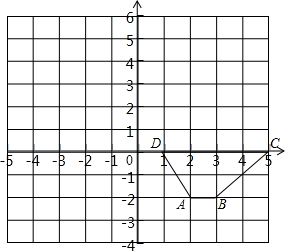 如图,在平面直角坐标系中,先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1
如图,在平面直角坐标系中,先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1