题目内容
 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以这两个交点和该抛物线的顶点、对称轴上一点为顶点的菱形称为这条抛物线的“抛物菱形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以这两个交点和该抛物线的顶点、对称轴上一点为顶点的菱形称为这条抛物线的“抛物菱形”.(1)若抛物线y=ax2+bx+c(a≠0)与x轴的两个交点为(-1,0)、
(3,0),且这条抛物线的“抛物菱形”是正方形,求这条抛物线的函数解析式;
(2)如图,四边形OABC是抛物线y=-x2+bx(b>0)的“抛物菱形”,且∠OAB=60°
①求“抛物菱形OABC”的面积.
②将直角三角板中含有“60°角”的顶点与坐标原点O重合,两边所在直线与“抛物菱形OABC”的边AB、BC交于E、F,△OEF的面积是否存在最小值,若存在,求出此时△OEF的面积;若不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)根据正方形的性质求得A点的坐标,然后根据待定系数法即可求得解析式;
(2)①根据“抛物菱形”的性质,依据∠OAB=60°求得OB的长,然后根据勾股定理求得AC的值,即可求得菱形的面积;②当三角板的两边分别垂直与AB和BC时三角形OEF的面积最小,从而求得△OEF是等边三角形,根据勾股定理求得OE=1,然后求边长为1的等边三角形的面积即可.
(2)①根据“抛物菱形”的性质,依据∠OAB=60°求得OB的长,然后根据勾股定理求得AC的值,即可求得菱形的面积;②当三角板的两边分别垂直与AB和BC时三角形OEF的面积最小,从而求得△OEF是等边三角形,根据勾股定理求得OE=1,然后求边长为1的等边三角形的面积即可.
解答:解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴的两个交点为(-1,0)、(3,0),四边形OABC是正方形,
∴A(1,2),
∴
解得:
∴抛物线的解析式为:y=-
x2+x+
;
(2)①∵由抛物线y=-x2+bx(b>0)可知OB=b,
∵∠OAB=60°,
∴A(
,
b),
代入y=-x2+bx得:
b=-(
)2+b•
,解得:b=2
,
∴OB=2
,AC=6,
∴“抛物菱形OABC”的面积=
OB•AC=6
;
②存在;
当三角板的两边分别垂直与AB和BC时三角形OEF的面积最小,
∵OE⊥AB,
∴∠EOB=
∠AOB=30°,
同理∠BOF=30°,
∵∠EOF=60°
∴OB垂直EF且平分EF,
∴三角形OEF是等边三角形,
∵OB=
,
∴OE=1,
∴OE=OF=EF=1,
∴△OEF的面积=
.
∴A(1,2),
∴
|
|
∴抛物线的解析式为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)①∵由抛物线y=-x2+bx(b>0)可知OB=b,
∵∠OAB=60°,
∴A(
| b |
| 2 |
| ||
| 2 |
代入y=-x2+bx得:
| ||
| 2 |
| b |
| 2 |
| b |
| 2 |
| 3 |
∴OB=2
| 3 |
∴“抛物菱形OABC”的面积=
| 1 |
| 2 |
| 3 |
②存在;
当三角板的两边分别垂直与AB和BC时三角形OEF的面积最小,
∵OE⊥AB,
∴∠EOB=
| 1 |
| 2 |
同理∠BOF=30°,
∵∠EOF=60°
∴OB垂直EF且平分EF,
∴三角形OEF是等边三角形,
∵OB=
2
| ||
| 3 |
∴OE=1,
∴OE=OF=EF=1,
∴△OEF的面积=
| ||
| 4 |
点评:本题考查了“抛物菱形”的性质,抛物线的顶点坐标,正方形的性质,等边三角形的性质,待定系数法求解析式,勾股定理的应用等.

练习册系列答案
相关题目
一个三角形两边长分别为4和7,第三边长是方程x2-6x+5=0的根,则这个三角形的周长是( )
| A、12 | B、12或16 |
| C、16 | D、20 |
下列事件中,属于随机事件的是( )
| A、太阳绕着地球转 |
| B、明天太阳从西方升起 |
| C、一个月有35天 |
| D、小米骑车经过某十字路口时遇到红灯 |
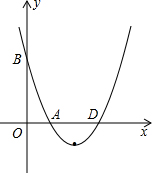 已知抛物线y=ax2+bx+c的图象经过点A(1,0),B(0,3),C(2,-1).
已知抛物线y=ax2+bx+c的图象经过点A(1,0),B(0,3),C(2,-1). 如图,在△ABC中,AB=AC=13,BC=10,D是边AC上一点,且tan∠DBC=
如图,在△ABC中,AB=AC=13,BC=10,D是边AC上一点,且tan∠DBC=