题目内容
6.以O为原点的平面直角坐标系中,x+y=100分别与直线y=3x,直线y=$\frac{1}{3}$x交于点A,B,求△ABO内坐标为整数的点(包括边界).分析 解两个函数的解析式组成的方程组即可求得交点A、B的坐标,然后根据S△ABO=S梯形ACDB+S△BDO-S△ACO列式计算求得三角形AOB的面积,就可求得整数点的个数.
解答  解:(1)由$\left\{\begin{array}{l}{x+y=100}\\{y=3x}\end{array}\right.$得$\left\{\begin{array}{l}{x=25}\\{y=75}\end{array}\right.$,
解:(1)由$\left\{\begin{array}{l}{x+y=100}\\{y=3x}\end{array}\right.$得$\left\{\begin{array}{l}{x=25}\\{y=75}\end{array}\right.$,
∴A(25,75);
由$\left\{\begin{array}{l}{x+y=100}\\{y=\frac{1}{3}x}\end{array}\right.$得$\left\{\begin{array}{l}{x=75}\\{y=25}\end{array}\right.$,
∴B(75,25);
∴S△ABO=S梯形ACDB+S△BDO-S△ACO,
∵S△BDO=S△ACO,
∴S△ABO=S梯形ACDB,
=$\frac{1}{2}$(25+75)(75-25)
=2500;
∴△ABO内坐标为整数的点(包括边界)有2500个.
点评 本题考查了两直线相交或平行问题,坐标与图形性质,三角形的面积,根据图形用梯形和直角三角形的面积表示出△ABO的面积是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列各式中正确的是( )
| A. | -(-2)>-1 | B. | |-0.2|=-0.2 | C. | |-5|<0 | D. | -$\frac{3}{2}$>-$\frac{1}{2}$ |
17.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后获毛利润共2.1万元(毛利润=(售价-进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量,已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,设甲种手机减少x部,求y的解析式.
(3)该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
| 甲 | 乙 | |
| 进价(元/部) | 4000 | 2500 |
| 售价(元/部) | 4300 | 3000 |
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量,已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,设甲种手机减少x部,求y的解析式.
(3)该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
4.下列化简正确的是( )
| A. | $\sqrt{27}$=9$\sqrt{3}$ | B. | $\sqrt{28}$=2$\sqrt{14}$ | C. | $\sqrt{\frac{7}{24}}$=$\frac{\sqrt{21}}{12}$ | D. | $\sqrt{\frac{3}{8}}$=$\frac{\sqrt{6}}{4}$ |
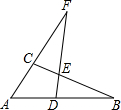 如图,△ABC中,D,E分别是AB和BC上的点,直线DE与AC的延长线交于点F,且AD•AB=AC•AF.求证:
如图,△ABC中,D,E分别是AB和BC上的点,直线DE与AC的延长线交于点F,且AD•AB=AC•AF.求证: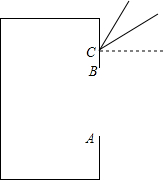 某地在一年中阳光与地面的最大角为60°,最小角为30°,当地的某一新建住宅区的住户准备统一在向阳的一边设计统一高度的窗,并在这些窗上方做一块“遮阳蓬”,如图所示.已知窗的统一高度AB为2米,试用你所学的知识,计算“遮阳蓬”CD应从窗的上方多高的点C伸出,伸出多长才能使房间内“冬暖夏凉”?
某地在一年中阳光与地面的最大角为60°,最小角为30°,当地的某一新建住宅区的住户准备统一在向阳的一边设计统一高度的窗,并在这些窗上方做一块“遮阳蓬”,如图所示.已知窗的统一高度AB为2米,试用你所学的知识,计算“遮阳蓬”CD应从窗的上方多高的点C伸出,伸出多长才能使房间内“冬暖夏凉”?