题目内容
16．
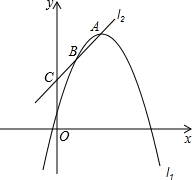如图，已知，抛物线l1：y=ax2-4ax+5+4a（a＜0）的顶点为A，直线l2：y=kx+3过点A，直线l2与抛物线l1及y轴分别交于B，C．（1）求k的值；
（2）若B为AC的中点，求a的值；
（3）在（2）的条件下，直接写出不等式ax2-4ax+5+4a＜kx+3的解集．
分析 （1）先把抛物线的解析式配成顶点式得到A点坐标，然后把A点坐标代入y=kx+3可求出k的值；
（2）先利用一次函数解析式求出C点坐标，再利用线段中点坐标公式得到B点坐标，然后把B点坐标代入y=a（x-2）2+5可求出a的值；
（3）观察图象，找出一次函数图象在抛物线上方所对应的自变量的取值范围即可得到不等式ax2-4ax+5+4a＜kx+3的解集．
解答 解：（1）∵y=ax2-4ax+5+4a=a（x-2）2+5，
∴顶点A的坐标为（2，5），
∵y=kx+3过点A（2，5），
∴2k+3=5，
∴k=1；
（2）∵一次函数的解析式为y=x+3，
∴C（0，3），
∵B为AC的中点，
∴B（1，4），
把B（1，4）代入y=a（x-2）2+5得a+5=4，
∴a=-1；
（3）不等式ax2-4ax+5+4a＜kx+3的解集为x＜1或x＞2．
点评 本题考查了二次函数综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会求抛物线与直线的交点坐标；会利用图象法解不等式；记住线段的中点坐标公式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．下列二次根式中，属于最简二次根式的是（ ）
| A． | $\sqrt{4a+8}$ | B． | $\sqrt{24}$ | C． | $\sqrt{14}$ | D． | $\sqrt{1.4}$ |
10．下列式子是分式的是（ ）
| A． | $\frac{x}{2}$ | B． | $\frac{x}{x+1}$ | C． | $\frac{x}{2}$+y | D． | $\frac{x}{3}+1$ |
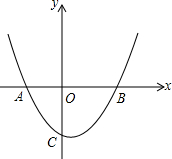如图，二次函数图象经过A（-3，0）、B（4，0）、C（0，-4）三点．
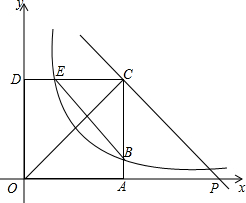如图所示，点A坐标为（4，0），矩形OACD的两边AC与CD分别交双曲线y=$\frac{4}{x}$（x＞0）于B，E两点，记$\frac{BC}{AB}$=k，过点C作CP∥BE交x轴于点P．
如图，正方形ABCD的边长为1，求阴影部分的面积？
