题目内容
如图,在平面直角坐标系中,矩形OABC的四个顶点坐标分别为O(0,0),A(4,0),B(4,3),C(0,3),G是对角线AC的中点,动直线MN平行于AC且交矩形OABC的一组邻边于E、F,交y轴、x轴于M、N.设点M的坐标为(0,t),△EFG的面积为S.
(1)求S与t的函数关系式;
(2)当△EFG为直角三角形时,求t的值;
(3)当点G关于直线EF的对称点G′恰好落在矩形OABC的一条边所在直线上时,直接写出t的值.
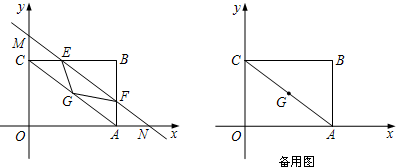
(1)求S与t的函数关系式;
(2)当△EFG为直角三角形时,求t的值;
(3)当点G关于直线EF的对称点G′恰好落在矩形OABC的一条边所在直线上时,直接写出t的值.

考点:四边形综合题
专题:
分析:(1)分为MN在CA的左下方(0<t<3)和右上方(3<t<6)两种情况;分别把EF表示出来,把△EFG的高表示出来即可;
(2)当0<t<3时,把△EFG三边的平方表示出来,△EFG是直角三角形有三种可能,列出三个方程,分别解出即可,同样当3<t<6时,把△EFG三边的平方表示出来,△EFG是直角三角形也有三种可能,同理解出t的值;
(3)GG′所在的直线与直线CA垂直,且过G点,故表达式为y=
x-
,分别求出直线GG′与直线CB、BA、OA、OC的交点G′的中点在直线MN上即可得到四种情况的答案.
(2)当0<t<3时,把△EFG三边的平方表示出来,△EFG是直角三角形有三种可能,列出三个方程,分别解出即可,同样当3<t<6时,把△EFG三边的平方表示出来,△EFG是直角三角形也有三种可能,同理解出t的值;
(3)GG′所在的直线与直线CA垂直,且过G点,故表达式为y=
| 4 |
| 3 |
| 7 |
| 6 |
解答:解:(1)①当0<t<3时,如图1,过E作EH⊥CA于H,

∵A(4,0),B(4,3),C(0,3),
∴OA=4,OC=3,AC=5,
∵MN∥CA,
∴△OEF∽△OCA,
∴OE:OC=EF:CA,即t:3=EF:5,
∴EF=
t,
∵EH⊥CA,
∴∠ECH=∠OCA,
∴sin∠ECH=sin∠OCA,
∴EG:EC=OA:CA,
即EH:(3-t)=4:5,
∴EH=
(3-t),
∴S=
×EF×HE=
×
t×
(3-t)=-
t2+2t;
②当3<t<6时,如图2,过C作CH⊥MN于H,则MC=t-3,
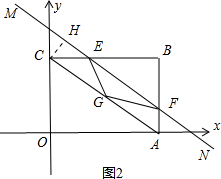
∵CH⊥MN,∴∠CMH=∠OCA,∴sin∠CMH=sin∠OCA,
∴CH:MC=OA:CA,即CH:(t-3)=4:5,
∴CH=
(t-3),
易求直线AC解析式为:y=-
x+3,
∵MN∥CA,
∴直线MN的解析式为:y=-
x+t,
令y=3,可得3=-
x+t,解得x=
(t-3)=
t-4,
∴E(
t-4,3),
在y=-
x+t中,令x=4可得:y=t-3,∴F(4,t-3),
∴EF=
=
(6-t),
S=
×EF×GH=
×
(t-3)=-
t2+6t-12;
综上可知S=
;
(2)①当0<t<3时,E(0,t),F(
t,0),G(2,
),
∴EF2=
t2,EG2=22+(t-
)2,GF2=(
t-2)2+(
)2,
若EF2+EG2=GF2,则有
t2+22+(t-
)2=(
t-2)2+(
)2,解得t=0(舍去),t=-
(舍去),
若EF2+FG2=EG2,则有
t2+(
t-2)2+(
)2=22+(t-
)2,解得t=0(舍去),t=
,
若EG2+GF2=EF2,则有22+(t-
)2+(
t-2)2+(
)2=
t2,解得t=
,
②当3<t<6时,E(
t-4,3),F(4,t-3),G(2,
),
∴EF2=(
t-8)2+(t-6)2,EG2=(
t-6)2+(
)2,GF2=22+(t-
)2,
若EF2+EG2=GF2,则有(
t-8)2+(t-6)2+(
t-6)2+(
)2=22+(t-
)2,整理得32t2-363t+1026=0,△=441,解得t=
,t=6(舍去),
若EF2+FG2=EG2,则有(
t-8)2+(t-6)2+22+(t-
)2=(
t-6)2+(
)2,整理得6t2-79t+258=0,△=49,解得t=6(舍去),t=
>6(舍去),
若EG2+GF2=EF2,则有(
t-6)2+(
)2+22+(t-
)2=(
t-8)2+(t-6)2,解得t=
,
综上可知当△EFG为直角三角形时,t=
或t=
或t=
或t=
;
(3)直线MN为y=-
x+t,G(2,
),
GG′所在的直线与直线CA垂直,且过G点,故表达式为y=
x-
,在y=
x-
中,
令x=0,可得:y=-
,∴G′(0,-
),GG′中点(1,
),代入直线MN为y=-
x+t,解得t=
,
令y=0,可得:x=
,∴G′(
,0),GG′中点(
,
),代入直线MN为y=-
x+t,解得t=
,
令x=4,可得:y=
,∴G′(4,
),GG′中点(3,
),代入直线MN为y=-
x+t,解得t=
,
令y=3,可得:x=
,∴G′(
,3),GG′中点(
,
),代入直线MN为y=-
x+t,解得t=
,
综上可知满足条件的t的值为
或
或
或
.

∵A(4,0),B(4,3),C(0,3),
∴OA=4,OC=3,AC=5,
∵MN∥CA,
∴△OEF∽△OCA,
∴OE:OC=EF:CA,即t:3=EF:5,
∴EF=
| 5 |
| 3 |
∵EH⊥CA,
∴∠ECH=∠OCA,
∴sin∠ECH=sin∠OCA,
∴EG:EC=OA:CA,
即EH:(3-t)=4:5,
∴EH=
| 4 |
| 5 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
| 4 |
| 5 |
| 2 |
| 3 |
②当3<t<6时,如图2,过C作CH⊥MN于H,则MC=t-3,

∵CH⊥MN,∴∠CMH=∠OCA,∴sin∠CMH=sin∠OCA,
∴CH:MC=OA:CA,即CH:(t-3)=4:5,
∴CH=
| 4 |
| 5 |
易求直线AC解析式为:y=-
| 3 |
| 4 |
∵MN∥CA,
∴直线MN的解析式为:y=-
| 3 |
| 4 |
令y=3,可得3=-
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
∴E(
| 4 |
| 3 |
在y=-
| 3 |
| 4 |
∴EF=
(
|
| 5 |
| 3 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
| 2 |
| 3 |
综上可知S=
|
(2)①当0<t<3时,E(0,t),F(
| 4 |
| 3 |
| 3 |
| 2 |
∴EF2=
| 25 |
| 9 |
| 3 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
若EF2+EG2=GF2,则有
| 25 |
| 9 |
| 3 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
| 7 |
| 3 |
若EF2+FG2=EG2,则有
| 25 |
| 9 |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 21 |
| 32 |
若EG2+GF2=EF2,则有22+(t-
| 3 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
| 25 |
| 9 |
| 3 |
| 2 |
②当3<t<6时,E(
| 4 |
| 3 |
| 3 |
| 2 |
∴EF2=(
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 9 |
| 2 |
若EF2+EG2=GF2,则有(
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 9 |
| 2 |
| 171 |
| 32 |
若EF2+FG2=EG2,则有(
| 4 |
| 3 |
| 9 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
| 43 |
| 6 |
若EG2+GF2=EF2,则有(
| 4 |
| 3 |
| 3 |
| 2 |
| 9 |
| 2 |
| 4 |
| 3 |
| 9 |
| 2 |
综上可知当△EFG为直角三角形时,t=
| 21 |
| 32 |
| 3 |
| 2 |
| 9 |
| 2 |
| 171 |
| 32 |
(3)直线MN为y=-
| 3 |
| 4 |
| 3 |
| 2 |
GG′所在的直线与直线CA垂直,且过G点,故表达式为y=
| 4 |
| 3 |
| 7 |
| 6 |
| 4 |
| 3 |
| 7 |
| 6 |
令x=0,可得:y=-
| 7 |
| 6 |
| 7 |
| 6 |
| 1 |
| 6 |
| 3 |
| 4 |
| 11 |
| 12 |
令y=0,可得:x=
| 7 |
| 8 |
| 7 |
| 8 |
| 23 |
| 16 |
| 3 |
| 4 |
| 3 |
| 4 |
| 117 |
| 64 |
令x=4,可得:y=
| 25 |
| 6 |
| 25 |
| 6 |
| 17 |
| 6 |
| 3 |
| 4 |
| 61 |
| 12 |
令y=3,可得:x=
| 25 |
| 8 |
| 25 |
| 8 |
| 41 |
| 16 |
| 9 |
| 4 |
| 3 |
| 4 |
| 267 |
| 64 |
综上可知满足条件的t的值为
| 11 |
| 12 |
| 117 |
| 64 |
| 61 |
| 12 |
| 267 |
| 64 |
点评:本题主要考查一次函数解析式和相似三角形的判定和性质、勾股定理和一元二次方程的综合应用,在(1)中能分别用t表示出△EFG中的底和高是解题的关键,在(2)中注意分情况讨论,在(3)中由条件得出GG′所在的直线与直线CA垂直,且过G点,是解题的关键.本题计算量比较大,且情况较多,较易漏掉其中一种情况.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
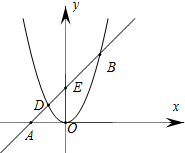 已知一次函数y=x+2与二次函数y=x2交于点D与B,y=x+2与x轴、y轴的交点分别为点A与点B,求S△ODB的值.
已知一次函数y=x+2与二次函数y=x2交于点D与B,y=x+2与x轴、y轴的交点分别为点A与点B,求S△ODB的值.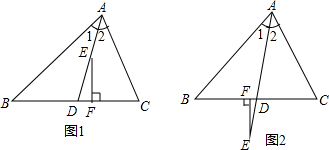
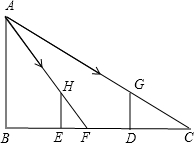 如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长.
如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长. 如图,已知AD为∠ABC中BC上中线,P为BD上一点,过P作AD的平行线交AB于点Q,交AC延长线于R,证明:PQ+PR=2AD.
如图,已知AD为∠ABC中BC上中线,P为BD上一点,过P作AD的平行线交AB于点Q,交AC延长线于R,证明:PQ+PR=2AD.