题目内容
16.已知二次函数y=-$\frac{1}{2}$x2-2x+1,当x<-2时,y随x的增大而增大.分析 把二次函数解析式化为顶点式,可求得其开口方向及对称轴,利用二次函数的增减性可求得答案.
解答 解:
∵y=-$\frac{1}{2}$x2-2x+1=-$\frac{1}{2}$(x+2)2+3,
∴抛物线开口向下,对称轴为x=-2,
∴当x<-2时,y随x的增大而增大,
故答案为:<-2.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.一元二次方程x2+x+2=0的根的情况是( )
| A. | 两个相等的实数根 | B. | 两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
4.用配方法解方程x2-2x-5=0时,原方程变形为( )
| A. | (x-1)2=6 | B. | (x+1)2=6 | C. | (x-2)2=9 | D. | (x+2)2=9 |
11.方程x(x-1)=0的解是( )
| A. | x=1 | B. | x1=0,x2=1 | C. | x=0 | D. | x1=0,x2=-1 |
6.若关于x的方程2m+x=1和方程3x-1=2x+1的解互为相反数,则m的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 0 | D. | -2 |
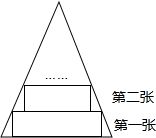 如图所示,一张等腰三角形纸片,底边长为18cm,底边上的高为18cm,现沿底边依次由下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是第5张.
如图所示,一张等腰三角形纸片,底边长为18cm,底边上的高为18cm,现沿底边依次由下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是第5张.