题目内容
14.下列二次根式中,属于最简二次根式的是( )| A. | $\sqrt{{x^2}+2}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{3}{2}}$ | D. | $\sqrt{4{a^3}{b^2}}$ |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:A、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故A正确;
B、被开方数含能开得尽方的因数或因式,故B错误;
C、被开方数含分母,故C错误;
D、被开方数含能开得尽方的因数或因式故D错误;
故选:A.
点评 本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.

练习册系列答案
相关题目
7.已知|x|=17,|y|=13,且xy<0,则|x-y|的值等于( )
| A. | 4 | B. | 30 | C. | 4或30 | D. | 4或0 |
9.张明的父母打算购买一种形状和大小都相同的正多边形瓷砖来铺地板,为了保证铺地板时既没缝隙,又不重叠,则所购瓷砖形状不能是( )
| A. | 正三角形 | B. | 正方形 | C. | 正六边形 | D. | 正八边形 |
19.关于x的一元二次方程mx2+(2m-1)x-2=0的根的判别式等于4,则m的值是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$或$-\frac{3}{2}$ |
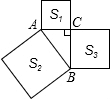 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1=9,S2=16,则S3=7.
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1=9,S2=16,则S3=7.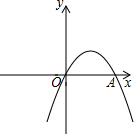 如图,抛物线y=-x2+bx+c经过坐标原点,并与x轴相交于点A(2,0).
如图,抛物线y=-x2+bx+c经过坐标原点,并与x轴相交于点A(2,0). 如图所示,直线AB、CD相交于点O,作∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=54°.
如图所示,直线AB、CD相交于点O,作∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=54°.