题目内容

20．二次函数y=x2+4x+7的最小值是（　　）
A．3B．4C．6D．7

分析 本题考查利用二次函数顶点式求最小（大）值的方法．

解答 解：∵原式可化为y=x2+4x+4+3=（x+2）2+3，
∴最小值为3．
故选：A．

点评 本题考查了二次函数的最值．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．

练习册系列答案
相关题目
5．下列科学计算器的按键中，其上面标注的符号是轴对称图形但不是中心对称图形的是（　　）
A．B．C．D．
11．在建设两型社会的过程中，为推进节能减排，发展低碳经济，我市某公司以25万元购得某项节能产品的生产技术后，再投入100万元购买生产设备，进行该产品的生产加工．已知生产这种产品的成本价为每件20元．经过市场调研发现，该产品的销售单价定在25元到30元之间较为合理，并且该产品的年销售量y（万件）与销售单价x（元）之间的函数关系式为：y=$\left\{\begin{array}{l}{40-x（25≤x≤30）}\\{25-0.5x（30＜x≤35）}\end{array}\right.$（年获利=年销售收入-生产收入-投资成本）
（1）当销售单价定为28元时，该产品的年销售量为多少万件？
（2）求该公司第一年的年获利W（万元）与销售单价x（元）之间的函数关系式，并说明投资的第一年，该公司是盈利还是亏损？若盈利，最大利润是多少？若亏损，最小亏损是多少？
（3）第二年，该公司决定给希望工程捐款Z万元，该项捐款由两部分组成：一部分为10万元的固定捐款；另一部分则为每销售一件产品，就抽出一元钱作为捐款．若除去第一年的最大获利（或最小亏损）以及第二年的捐款后，到第二年年底，两年的总盈利不低于67.5万元，请你确定此时销售单价的范围．
8．如图，△ABC内接于半圆O，AB为⊙O直径，点D是$\widehat{AC}$的中点，DE⊥AB于点E，且交AC于点P，连结AD．
（1）求证：AP=DP．
（2）若⊙O的半径为5，AD=6，求DP的长．
15．按照山西省“改薄工程”规划，我省5年投入85亿元用于改造农村县（市、区）薄弱学校，促进义务教育均衡发展，其中某项“改薄工程”建设，甲队单独完成需要20天，若由甲队先做13天，则剩下的工程由甲、乙两队合作3天完成．问乙队单独完成这项工程需要多少天？若设乙队单独完成这项工程需要x天，根据题意可列方程为（　　）
A．13+3+x=20B．$\frac{13}{20}$+3（$\frac{1}{20}$+$\frac{1}{x}$）=1C．$\frac{13}{20}$+$\frac{3}{x}$=1D．（1-$\frac{13}{20}$）+x=3
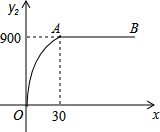5．成都地铁规划到2020年将通车13条线路，近几年正是成都地铁加紧建设和密集开通的几年，市场对建材的需求量有所提高，根据市场调查分析可预测：投资水泥生产销售后所获得的利润y1（万元）与投资资金量x（万元）满足正比例关系y1=20x；投资钢材生产销售的后所获得的利润y2（万元）与投资资金量x（万元）满足函数关系的图象如图所示（其中OA是抛物线的一部分，A为抛物线的顶点，AB∥x轴）．
（1）直接写出当0＜x＜30及x＞30时，y2与x之间的函数关系式；
（2）某建材经销公司计划投资100万元用于生产销售水泥和钢材两种材料，若设投资钢材部分的资金量为t（万元），生长销售完这两种材料后获得的总利润为W（万元）．
①求W与t之间的函数关系式；
②若要求投资钢材部分的资金量不得少于45万元，那么当投资钢材部分的资金量为多少万元时，获得的总利润最大？最大总利润是多少？
12．不透明袋子中装有2个红球，3个白球和a个黄球，这些球除颜色外无其他差别，若从这个袋子中随机摸出1个球是红球的概率为$\frac{1}{5}$，则黄球的个数为5个．
9．如图1，在四边形ABCD中，M为AD边上一点，∠ABM=∠MCD=90°，点E、F分别为边AM、DM的中点．
（1）求证：AD=2（BE+CF）．
（2）如图2，已知AB=3，$BD=3\sqrt{6}$，$AD=5\sqrt{3}$，∠BMC=2∠A．
①求证：△ABM∽△DCM；
②求BM+CM的值．
10．要使式子$\frac{{\sqrt{x-1}}}{x-3}$-x+2有意义，则x的取值范围是（　　）
A．x＞1B．x≥1C．x≥1且x≠3D．x≥3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网