题目内容
8. 如图,△ABC内接于半圆O,AB为⊙O直径,点D是$\widehat{AC}$的中点,DE⊥AB于点E,且交AC于点P,连结AD.
如图,△ABC内接于半圆O,AB为⊙O直径,点D是$\widehat{AC}$的中点,DE⊥AB于点E,且交AC于点P,连结AD.(1)求证:AP=DP.
(2)若⊙O的半径为5,AD=6,求DP的长.
分析 (1)作辅助线,构建直角△ADB,得∠2与∠DAB互余,由DE⊥AB得∠3与∠DAB互余,由等弧所对的圆周角相等得∠1=∠2,根据等量代换得∠1=∠3,再由等角对等边得AP=DP;
(2)先由勾股定理求DB=8,再根据面积相等求斜边上的高DE的长;由相似得AE的长,最后在直角△ADE中设PD=x,由勾股定理列方程,可求出x的值,即是PD的长.
解答  证明:(1)连接BD,
证明:(1)连接BD,
∵$\widehat{AD}$=$\widehat{DC}$,
∴∠1=∠2,
∵AB为⊙O直径,
∴∠ADB=90°,
∴∠2+∠DAB=90°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠3+∠DAE=90°,
∴∠2=∠3,
∴∠1=∠3,
∴DP=AP;
(2)由勾股定理得:DB=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
由S△ADB=$\frac{1}{2}$×AD×BD=$\frac{1}{2}$×AB×DE,
$\frac{1}{2}$×6×8=$\frac{1}{2}$×10×DE
∴DE=4.8,
∵∠2=∠3,∠AED=∠ADB,
∴△AED~△ADB,
∴$\frac{AE}{AD}$=$\frac{AD}{AB}$,
∴$\frac{AE}{6}=\frac{6}{10}$,
∴AE=3.6,
设PD=x,则AP=x,PE=4.8-x,
由勾股定理得:x2=3.62+(4.8-x)2,
x=3.75,
∴PD=3.75.
点评 本题考查了三角形的外接圆、等腰三角形的性质和勾股定理等知识的综合应用;同时还运用了面积法求高,这在数学中经常运用,要熟练掌握.

练习册系列答案
相关题目
13.甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是( )
| 队员 | 平均成绩 | 方差 |
| 甲 | 9.7 | 2.12 |
| 乙 | 9.6 | 0.56 |
| 丙 | 9.7 | 0.56 |
| 丁 | 9.6 | 1.34 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
3.某校8名学生参加了体育兴趣小组,他们被分成A、B两组进行训练,身高(单位:cm)如表所示:
设两队队员身高的平均数依次为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,方差依次为s甲2,s乙2,则下列关系中完全正确的是( )
| 队员1 | 队员2 | 队员3 | 队员4 | |
| 甲组 | 176 | 177 | 175 | 176 |
| 乙组 | 178 | 175 | 177 | 174 |
| A. | $\overline{x}$甲=$\overline{x}$乙,S甲2<S乙2 | B. | $\overline{x}$甲=$\overline{x}$乙,S甲2>S乙2 | ||
| C. | $\overline{x}$甲>$\overline{x}$乙,S甲2<S乙2 | D. | $\overline{x}$甲>$\overline{x}$乙,S甲2>S乙2 |
20.二次函数y=x2+4x+7的最小值是( )
| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
18.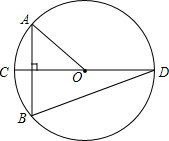 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
 如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).
如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).