题目内容
12.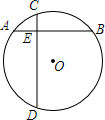 在⊙O中,弦AB⊥CD,垂足为E,且AE=3cm,BE=7cm,CE=3cm,ED=9cm,求⊙O的半径.
在⊙O中,弦AB⊥CD,垂足为E,且AE=3cm,BE=7cm,CE=3cm,ED=9cm,求⊙O的半径.
分析 过点O分别作AB、CD的垂线OM、ON,则四边形OMEN是矩形,利用垂径定理即可求得OM,BM的长度,然后在直角△BOM中利用勾股定理即可求得OB的长度.
解答 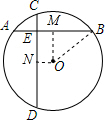 解:过点O分别作AB、CD的垂线OM、ON,则四边形OMEN是矩形,连接OB.
解:过点O分别作AB、CD的垂线OM、ON,则四边形OMEN是矩形,连接OB.
∵AE=3cm,BE=7cm,CE=3cm,ED=9cm,∴CD=2+6=8,
∵ON⊥CD
∴CN=$\frac{1}{2}$CD=6,
∴EN=OM=3,
同理:BM=5.
在直角△BMO中,OB=$\sqrt{O{M}^{2}+B{M}^{2}}$=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
∴⊙O的半径为$\sqrt{34}$.
点评 此题考查了垂径定理,勾股定理,相似三角形的判定与性质,以及矩形的判定与性质,根据图形作出相应的辅助线是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.一元二次方程(x-4)2=2x-3化为一般式是( )
| A. | x2-10x+13=0 | B. | x2-10x+19=0 | C. | x2-6x+13=0 | D. | x2-6x+19=0 |
20.缸内红茶菌的面积每天长大一倍,若16天长满整个缸面,那么经过( )天长满缸面的一半.
| A. | 8 | B. | 9 | C. | 16 | D. | 15 |
17.抛物线y=2(x+3)2-4的顶点坐标是( )
| A. | (3,4) | B. | (-3,4) | C. | (-3,-4) | D. | (3,-4) |
 如图,在斜坡的顶部有一铁塔AB,在阳光的照射下,塔影DE留在坡面上,已知铁塔底座宽CD=12m,塔影长DE=27m,小明和小华的身高都是1.6m,小明站在点E处,影子也在斜坡面上,小华站在沿DE方向的坡脚下,影子在平地上,两人的影长分别为3m和1.5m,那么塔高AB=20.8m.
如图,在斜坡的顶部有一铁塔AB,在阳光的照射下,塔影DE留在坡面上,已知铁塔底座宽CD=12m,塔影长DE=27m,小明和小华的身高都是1.6m,小明站在点E处,影子也在斜坡面上,小华站在沿DE方向的坡脚下,影子在平地上,两人的影长分别为3m和1.5m,那么塔高AB=20.8m.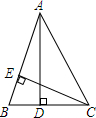 如图,在△ABC中,AD,CE是△ABC的高,找出图中的一组比例线段,并说明理由.
如图,在△ABC中,AD,CE是△ABC的高,找出图中的一组比例线段,并说明理由.