题目内容
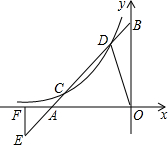 已知直线y=x+3与x轴、y轴分别交于A,B点,与y=
已知直线y=x+3与x轴、y轴分别交于A,B点,与y=| k |
| x |
| 7 |
| 2 |
考点:反比例函数与一次函数的交点问题
专题:
分析:先求出A、B两个点的坐标,再设C点的坐标为(x1,x1+3),D点的坐标为(x2,x2+3)(x1<x2),联立y=x+3与y=
,则x1、x2是一元二次方程x2+3x-k=0的两个根,根据方程根的定义及一元二次方程根与系数的关系,并结合已知面积的条件即可求出k的值.
| k |
| x |
解答:解:∵直线y=x+3与x轴、y轴分别交于A、B点,
∴A(-3,0),B(0,3).
把y=x+3代入y=
,整理,得x2+3x-k=0.
设C点的坐标为(x1,x1+3),D点的坐标为(x2,x2+3)(x1<x2),
则x1、x2是一元二次方程x2+3x-k=0的两个根,
∴x1+x2=-3,x12+3x1-k=0 ①.
∵△AOD的面积+△AEF的面积=
,
∴
×3×(x2+3)+
(3+x1)(x1+3)=
,
∴3x2+9+x12+6x1+9=7,
将①代入上式,得k+9=7,
∴k=-2,
故答案为:-2.
∴A(-3,0),B(0,3).
把y=x+3代入y=
| k |
| x |
设C点的坐标为(x1,x1+3),D点的坐标为(x2,x2+3)(x1<x2),
则x1、x2是一元二次方程x2+3x-k=0的两个根,
∴x1+x2=-3,x12+3x1-k=0 ①.
∵△AOD的面积+△AEF的面积=
| 7 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
∴3x2+9+x12+6x1+9=7,
将①代入上式,得k+9=7,
∴k=-2,
故答案为:-2.
点评:本题考查了一次函数与反比例函数的交点、方程根的定义、一元二次方程根与系数的关系及三角形的面积公式,综合性较强,难度中等.

练习册系列答案
相关题目
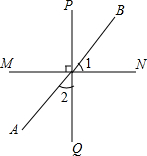 如图,直线PQ⊥MN,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为( )
如图,直线PQ⊥MN,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为( )| A、50° | B、40° |
| C、60° | D、70° |
二次函数y=ax2+bx+c的自变量x与函数y的对应值如下表,可判断二次函数的图象与x轴( )
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 1 | -2 | -3 | -2 | … |
| A、只有一个公共点 |
| B、有两个交点,且它们分别在y轴两侧 |
| C、有两个交点,且它们均在y轴同侧 |
| D、无公共点 |
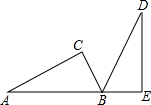 如图,将一个直角三角板ACB(∠C=90°)绕60°角的顶点B顺时针旋转,使得点C旋转到AB的延长线上的点E处,请解答下列问题:
如图,将一个直角三角板ACB(∠C=90°)绕60°角的顶点B顺时针旋转,使得点C旋转到AB的延长线上的点E处,请解答下列问题: 如图,⊙O是△ABC的外接圆,∠A=40°,则∠OCB等于
如图,⊙O是△ABC的外接圆,∠A=40°,则∠OCB等于